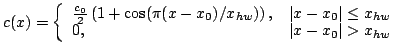Initial Conditions

The 1D wave equation is a second order (in time) partial differential equation, and as such, requires two initial conditions. Normally these are the values of the variable 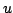$u$ and its time derivative, at time 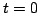$t=0$, i.e.,

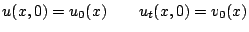$$u(x,0) = u_{0}(x)\qquad u_{t}(x,0) = v_{0}(x)$$ (6.4)

Other equivalent choices (such as wave variables which are of use in a digital waveguide implementation) are possible.

In some physical modeling synthesis applications, such as for the modeling of struck or plucked strings, it is convenient in the first instance to initialize the model itself using the above conditions. For a strike, for instance, one could choose a function 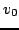$v_{0}$, perhaps peaked at a desired location corresponding to the strike center. For a pluck, one could make a similar choice for 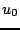$u_{0}$. One particular artificial (but physically reasonable) choice of initial condition profile, characterized by a small number of parameters, is the raised cosine distribution, defined by

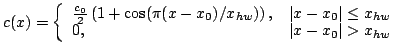$$c(x) = \left\{\begin{array}{lr} \frac{c_{0}}{2}\left(1+\cos(\pi(... ...x-x_{0}\vert\leq x_{hw}\\ 0, & \vert x-x_{0}\vert> x_{hw} \end{array}\right.$$ (6.5)

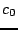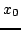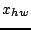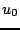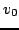Here, $c_{0}$ is the peak amplitude, $x_{0}$ the spatial center, and $x_{hw}$ the half-width length of the distribution. Such a function may be used in order to set either $u_{0}$ or $v_{0}$, or both, and may be used generally across a wide variety of 1D physical systems. It may also be extended in a natural way to two dimensions. In a more complete physical modeling framework, however, generally such interactions are modeled not through initialization, but through applied forces, perhaps from a hammer or hand model.