




Next: Initial Conditions
Up: Definition
Previous: Definition
Contents
Index
Non-dimensionalization is an extremely useful means of simplifying physical systems, especially in preparation for the application of numerical simulation techniques. As a first step, one may introduce the dimensionless coordinate 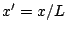 , for some constant
, for some constant 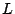 with dimensions of length. In the general case of the wave equation defined over an arbitrary spatial domain
with dimensions of length. In the general case of the wave equation defined over an arbitrary spatial domain
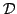 , this constant is arbitrary, but over a finite spatial domain, such as
, this constant is arbitrary, but over a finite spatial domain, such as
![$ x\in[0,x_{0}]$](img397.png) , it may be taken to be the length
, it may be taken to be the length 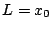 , thus yielding a system defined over the domain
, thus yielding a system defined over the domain
![$ x'\in[0,1]$](img399.png) . The wave equation (6.1) then becomes, in primed coordinates,
. The wave equation (6.1) then becomes, in primed coordinates,
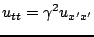 |
(6.2) |
where
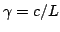 is a constant with dimensions of frequency. Such a description is useful in relating the wave equation to the simple harmonic oscillator, as described in Chapter 3. This is also a good example of a reduction in the number of parameters necessary to specify a system, which is of particular importance in physical modeling sound synthesis--it is redundant to specify both
is a constant with dimensions of frequency. Such a description is useful in relating the wave equation to the simple harmonic oscillator, as described in Chapter 3. This is also a good example of a reduction in the number of parameters necessary to specify a system, which is of particular importance in physical modeling sound synthesis--it is redundant to specify both  and
and 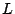 , and the single parameter
, and the single parameter 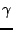 suffices. The fewer in number the parameters, the easier it will be for the musician working with a synthesis algorithm to navigate the space of possible timbres. In general, forms in this book will be presented, whenever possible, in such a spatially-nondimensionalized form, and the primed notation will be suppressed.
suffices. The fewer in number the parameters, the easier it will be for the musician working with a synthesis algorithm to navigate the space of possible timbres. In general, forms in this book will be presented, whenever possible, in such a spatially-nondimensionalized form, and the primed notation will be suppressed.
In the standard numerical analysis literature, it is commonplace to see a further temporal nondimensionalization, through the introduction of a temporal variable 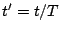 , for a characteristic time constant
, for a characteristic time constant 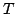 . A judicious choice of
. A judicious choice of
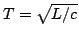 leads to the form
leads to the form
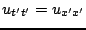 |
(6.3) |
Though this form is apparently simpler than (6.2) above, in practice, especially when programming synthesis routines, there is no real advantage to such a further step (i.e., an extra parameter, namely the time step, will be re-introduced during the discretization procedure). In addition, the crucial frequency domain behaviour of such a fully nondimensionalized system is slightly obscured through the introduction of such temporal scaling. For this reason, only ``half-way" spatial nondimensionalization will be employed in this book.





Next: Initial Conditions
Up: Definition
Previous: Definition
Contents
Index
Stefan Bilbao
2006-11-15
![]() , for some constant
, for some constant ![]() with dimensions of length. In the general case of the wave equation defined over an arbitrary spatial domain
with dimensions of length. In the general case of the wave equation defined over an arbitrary spatial domain
![]() , this constant is arbitrary, but over a finite spatial domain, such as
, this constant is arbitrary, but over a finite spatial domain, such as
![]() , it may be taken to be the length
, it may be taken to be the length ![]() , thus yielding a system defined over the domain
, thus yielding a system defined over the domain
![]() . The wave equation (6.1) then becomes, in primed coordinates,
. The wave equation (6.1) then becomes, in primed coordinates,
![]() , for a characteristic time constant
, for a characteristic time constant ![]() . A judicious choice of
. A judicious choice of
![]() leads to the form
leads to the form