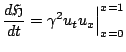Next: Bounds on Solution Size
Up: Definition
Previous: Energy Analysis
Contents
Index
The 1D wave equation involves second-order differentiation in space, and, as such, requires the specification of a single boundary condition at any endpoint of the spatial domain. A typical such condition often employed at an endpoint, such as  , of the domain is the following:
, of the domain is the following:
 |
(6.20) |
Such a condition is often referred to as being of Dirichlet type. If the 1D wave equation is intended to describe the displacement of a string, then this is clearly a fixed termination. If 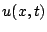 represents the pressure variation in an acoustic tube, such a condition corresponds to an open end of the tube.
represents the pressure variation in an acoustic tube, such a condition corresponds to an open end of the tube.
Another commonly-occurring condition is the Neumann condition:
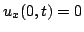 |
(6.21) |
Such a condition is easily interpreted in the context of the acoustic tube as corresponding to a closed tube end, and less easily in the case of string, where it may be viewed as describing a string endpoint which is free to move in a transverse direction.
Both conditions are lossless--in order to get a better idea of what this means (and to gain some insights into how such conditions may be arrived at), energy techniques are invaluable. Consider now the wave equation defined not over the infinite domain
 , but over the semi-infinite domain6.1
, but over the semi-infinite domain6.1
![$ {\mathcal D} = {\mathbb{R}}^{+}=[0,\infty]$](img436.png) . Taking an inner product of the wave equation with
. Taking an inner product of the wave equation with 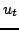 , now over the semi-infinite domain gives (
, now over the semi-infinite domain gives (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) as before, but integration by parts yields, instead of (
) as before, but integration by parts yields, instead of (![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
),
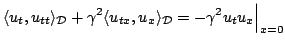 |
(6.22) |
An extra boundary term has thus appeared, and one can thus not proceed in general to a statement of conservation of energy such as (6.16), but rather
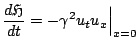 |
(6.23) |
Now, the lossless interpretation of the Dirichlet and Neumann conditions above should be clear; the boundary term vanishes in either case, and one again has exact energy conservation. (Note, however, that in the case of the Dirichlet condition, the true losslessness condition, from the above, is rather that 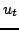 vanish at the boundary, which is in fact implied by the more realistic condition that
vanish at the boundary, which is in fact implied by the more realistic condition that 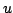 itself vanish.)
itself vanish.)
The Dirichlet and Neumann conditions are by no means the only possible boundary conditions for the wave equation; there is in fact an infinite number of possible terminations, some of which possess a physical interpretation. For example, a simple lossy condition is given by the so-called Robin type condition,
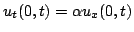 |
(6.24) |
for some constant 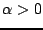 . In this case, one clearly has
. In this case, one clearly has
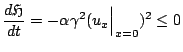 |
(6.25) |
implying that the energy is in fact monotonically decreasing. It becomes very simple, using energetic techniques, to categorize sources of loss according to whether they occur at the boundary, or over the problem interior. When translated to a numerical setting, it becomes similarly possible to isolate potential sources of numerical instability--some are of global type, occurring over the problem interior, but often instability originates at an improperly set numerical boundary condition.
One can go much further along these lines, and analyze nonlinear boundary conditions, as well as potentially energetic transfer to another object connected at the problem boundary. Some examples appear in problem ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
.
Also, it follows directly that when the spatial domain of the problem at hand is finite, e.g., if
![$ {\mathcal D}=[0,1]$](img441.png) , as is the case in all musical systems of interest, the energy balance becomes
, as is the case in all musical systems of interest, the energy balance becomes
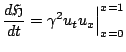 |
(6.26) |
The boundary conditions at both ends of the domain come into play.





Next: Bounds on Solution Size
Up: Definition
Previous: Energy Analysis
Contents
Index
Stefan Bilbao
2006-11-15
![]() , of the domain is the following:
, of the domain is the following:
![]() , but over the semi-infinite domain6.1
, but over the semi-infinite domain6.1
![]() . Taking an inner product of the wave equation with
. Taking an inner product of the wave equation with ![]() , now over the semi-infinite domain gives (
, now over the semi-infinite domain gives (![]() ) as before, but integration by parts yields, instead of (
) as before, but integration by parts yields, instead of (![]() ),
),
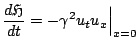
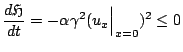
![]() .
.
![]() , as is the case in all musical systems of interest, the energy balance becomes
, as is the case in all musical systems of interest, the energy balance becomes