




Next: Modes
Up: Definition
Previous: Boundary Conditions
Contents
Index
Under conservative conditions, the bounds (6.19) hold, regardless of whether
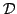 , the spatial domain, is defined as the entire
, the spatial domain, is defined as the entire 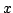 axis, a semi-infinite domain, or a finite interval. It is important to note that both such bounds apply to derivatives of the dependent variable, and not the dependent variable itself. This is in direct contrast to the case of the harmonic oscillator, and might seem counterintuitive, but follows directly from the definition of the 1D wave equation itself: note that second-derivatives only appear, so that any solution of the form
axis, a semi-infinite domain, or a finite interval. It is important to note that both such bounds apply to derivatives of the dependent variable, and not the dependent variable itself. This is in direct contrast to the case of the harmonic oscillator, and might seem counterintuitive, but follows directly from the definition of the 1D wave equation itself: note that second-derivatives only appear, so that any solution of the form
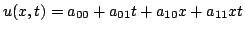 |
(6.27) |
automatically satisfies the wave equation for any constants 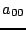 ,
, 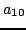 ,
, 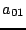 and
and 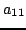 , and such a solution can clearly not be bounded for all
, and such a solution can clearly not be bounded for all 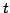 and all
and all 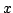 . The wave equation, unless properly terminated, allows a solution which is capable of drifting.
. The wave equation, unless properly terminated, allows a solution which is capable of drifting.
Nevertheless, conditions may indeed be employed to derive bounds of a less strict type on the size of the solution itself. Take, for instance, instance, the first of conditions (6.19). One may write
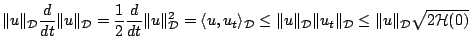 |
(6.28) |
where the first inequality above follows from the Cauchy-Schwartz inequality, and the second is results from the first of bounds (6.19). One thus has
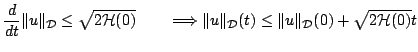 |
(6.29) |
and the norm of the solution at time 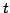 is bounded by an affine function of time
is bounded by an affine function of time 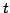 ; growth is no faster than linear.
; growth is no faster than linear.
As one might expect, better bounds are possible if fixed boundary conditions are employed. Considering again the wave equation defined over the semi-infinite domain
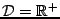 , with the Dirichlet condition (6.20) applied at
, with the Dirichlet condition (6.20) applied at 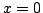 , one has, at any point
, one has, at any point 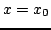 ,
,
![$\displaystyle \vert u(x_{0},t)\vert = \vert\int_{x=0}^{x=x_{0}}u_{x}(x,t)dx'\ve...
... D}}\Vert 1\Vert _{[0,x_{0}]} \leq \frac{1}{\gamma}\sqrt{2{\mathcal H}(0)x_{0}}$](img452.png) |
(6.30) |
The magnitude of the solution at any point 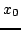 in the semi-infinite domain may thus be bounded in terms of its distance from the end point. Notice that this is in fact a much stronger condition than a bound on the norm of the solution (in fact, it is such a bound, but in a Chebyshev, or
in the semi-infinite domain may thus be bounded in terms of its distance from the end point. Notice that this is in fact a much stronger condition than a bound on the norm of the solution (in fact, it is such a bound, but in a Chebyshev, or
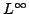 type norm. If the spatial domain
type norm. If the spatial domain
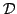 above is changed to the finite interval
above is changed to the finite interval
![$ {\mathcal D}=[0,1]$](img441.png) , the above analysis is unchanged, and, as long as the boundary condition at
, the above analysis is unchanged, and, as long as the boundary condition at 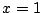 is conservative, one may go further and write
is conservative, one may go further and write
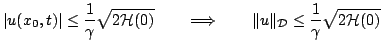 |
(6.31) |
which is indeed a bound on the 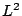 norm of the solution. If the boundary condition at
norm of the solution. If the boundary condition at 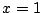 is of Dirichlet type, an improved bound is possible. See Problem 6.1.
is of Dirichlet type, an improved bound is possible. See Problem 6.1.





Next: Modes
Up: Definition
Previous: Boundary Conditions
Contents
Index
Stefan Bilbao
2006-11-15
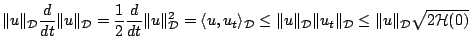
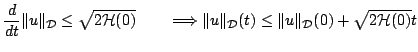
![]() , with the Dirichlet condition (6.20) applied at
, with the Dirichlet condition (6.20) applied at ![]() , one has, at any point
, one has, at any point ![]() ,
,
![$\displaystyle \vert u(x_{0},t)\vert = \vert\int_{x=0}^{x=x_{0}}u_{x}(x,t)dx'\ve...
... D}}\Vert 1\Vert _{[0,x_{0}]} \leq \frac{1}{\gamma}\sqrt{2{\mathcal H}(0)x_{0}}$](img452.png)