




Next: Hughes-Taylor and Newmark Methods
Up: Other Schemes
Previous: Using Time-averaging Operators
Contents
Index
A Second-order Family of Schemes
Though the stability condition inherent in scheme (3.18) has been circumvented in scheme (3.42), the problem of warped frequency persists. Using combination properties of the averaging operators, discussed in Section 2.2, it is not difficult to see that any scheme of the form
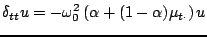 |
(3.51) |
will also be a second-order accurate approximation to (3.1), for any choice of the real parameter 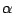 . In fact, it would be better to say ``at least second-order accurate"--see Section 3.3.4 for more discussion. There is thus a one-parameter family of schemes for (3.1), all of which operate as two step recursions: written out in full, the recursion has the form
. In fact, it would be better to say ``at least second-order accurate"--see Section 3.3.4 for more discussion. There is thus a one-parameter family of schemes for (3.1), all of which operate as two step recursions: written out in full, the recursion has the form
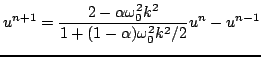 |
(3.52) |
Schemes (3.18) and (3.42) are members of this family with
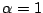 and
and
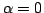 , respectively.
, respectively.
It is interesting to examine the frequency warping characteristics of various members of this family, as function of
 , the reference frequency for the simple harmonic oscillator. In Figure 3.3, the frequency
, the reference frequency for the simple harmonic oscillator. In Figure 3.3, the frequency 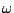 of the scheme (3.51) is plotted as a function of reference frequency
of the scheme (3.51) is plotted as a function of reference frequency
 , for different choices of
, for different choices of 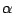 . Notice that for small values of
. Notice that for small values of 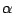 , lower than about
, lower than about
 , the difference scheme frequency is artificially low, and for values closer to
, the difference scheme frequency is artificially low, and for values closer to 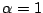 , artificially high. In fact, for high values of
, artificially high. In fact, for high values of 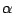 , there is a certain ``cutoff" frequency
, there is a certain ``cutoff" frequency
 , for which the difference scheme becomes unstable--this is readily visible in the figure. In the middle range of values of
, for which the difference scheme becomes unstable--this is readily visible in the figure. In the middle range of values of 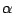 (between about
(between about
 and
and
 ), the difference scheme yields a good approximation over nearly the entire range of frequencies
), the difference scheme yields a good approximation over nearly the entire range of frequencies
 up to the Nyquist limit. It is useful, from a musical point of view, to plot the frequency deviation in terms of cents, defined as
up to the Nyquist limit. It is useful, from a musical point of view, to plot the frequency deviation in terms of cents, defined as
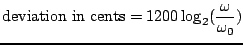 |
(3.53) |
A deviation of 100 cents corresponds to a musical interval of a semitone.
which is shown in Figure 3.3(b). For low values of
Figure:
(a), frequency 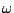 of the parameterized difference scheme (3.51) for the simple harmonic oscillator (3.1), plotted against
of the parameterized difference scheme (3.51) for the simple harmonic oscillator (3.1), plotted against
 as dotted lines, for various values of the free parameter
as dotted lines, for various values of the free parameter 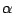 (indicated in the figure). The reference frequency is plotted as a solid black line. (b), deviation in cents of
(indicated in the figure). The reference frequency is plotted as a solid black line. (b), deviation in cents of 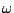 from
from
 for the same members of the family, as a function of
for the same members of the family, as a function of
![$ \omega _{0}\in [0, \frac {\pi }{k}]$](img45.png) . Zero deviation is plotted as a solid black line. Successive deviations of a musical semitone are indicated by grey horizontal lines.
. Zero deviation is plotted as a solid black line. Successive deviations of a musical semitone are indicated by grey horizontal lines.
 |





Next: Hughes-Taylor and Newmark Methods
Up: Other Schemes
Previous: Using Time-averaging Operators
Contents
Index
Stefan Bilbao
2006-11-15
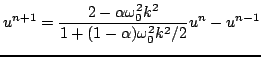
![]() , the reference frequency for the simple harmonic oscillator. In Figure 3.3, the frequency
, the reference frequency for the simple harmonic oscillator. In Figure 3.3, the frequency ![]() of the scheme (3.51) is plotted as a function of reference frequency
of the scheme (3.51) is plotted as a function of reference frequency
![]() , for different choices of
, for different choices of ![]() . Notice that for small values of
. Notice that for small values of ![]() , lower than about
, lower than about
![]() , the difference scheme frequency is artificially low, and for values closer to
, the difference scheme frequency is artificially low, and for values closer to ![]() , artificially high. In fact, for high values of
, artificially high. In fact, for high values of ![]() , there is a certain ``cutoff" frequency
, there is a certain ``cutoff" frequency
![]() , for which the difference scheme becomes unstable--this is readily visible in the figure. In the middle range of values of
, for which the difference scheme becomes unstable--this is readily visible in the figure. In the middle range of values of ![]() (between about
(between about
![]() and
and
![]() ), the difference scheme yields a good approximation over nearly the entire range of frequencies
), the difference scheme yields a good approximation over nearly the entire range of frequencies
![]() up to the Nyquist limit. It is useful, from a musical point of view, to plot the frequency deviation in terms of cents, defined as
up to the Nyquist limit. It is useful, from a musical point of view, to plot the frequency deviation in terms of cents, defined as
