Natural Decay of the String

Figure 14: An extension of our simple digital waveguide by including loss through a loop filter. Note that the inverters between the delay lines are only present when acceleration, velocity and displacement of the string is modeled.

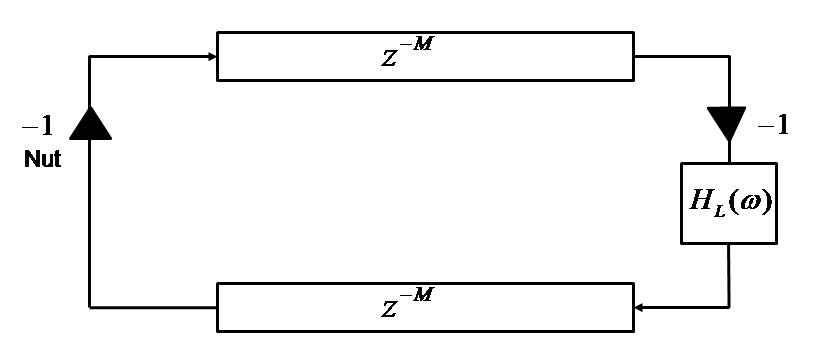
If a physical string is tied to two rigid ends, energy injected into the string remains within the string. However, it does eventually stop motion. The tension of the string, friction with the air and various effects cause the string's motion to eventually stop [7]. By inserting a low-pass filter into the digital waveguide, as shown in Figure 14, we can model the string's decay properties in our virtual model [8]. Computing the loop filter's coefficients is discussed in Section 4.2.2.

Extending our simple digital waveguide, as shown in Figure 14 we add the string's damping into the Waveguide's feedback loop. This maps physically to energy loss in the string from friction, the string's properties and other more minute, time-invariant effects.

We use a frequency all-pass filter $H_L(\omega)$ to calibrate our Waveguide to match the decay as measured from a real guitar string. In the context of a digital waveguide, $H_L(\omega)$ is called the loop filter.