Modeling Two Planes of Vibration

Figure 15: Two linearly coupled digital waveguides. Each Waveguide represents one plane of motion of the string. The vertical plane denotes the transverse direction with respect to the body of the instrument. $H_{vv}$ corresponds to the strings interaction with the instrument's body. $H_{vh}$ and $H_{hv}$ correspond to the coupling between the string in its two orthogonal planes of motion.

In the physical world, the strings of an instrument vibrate in two orthogonal planes. In previous sections, we discussed modeling vibrations of the string with a single digital waveguide. To a first approximation, the single digital waveguide representing the transverse motion of the string is accurate, as most energy transferred to the body of the instrument occurs in a single plane. However, to capture more peculiar phenomena, it is necessary to use two digital waveguides, each representing two orthogonal planes of motion. With two digital waveguides and a full covariance-matrix correlating both waveguides, effects such as Two-Stage Decay and beating effects can be correctly modeled [9]. 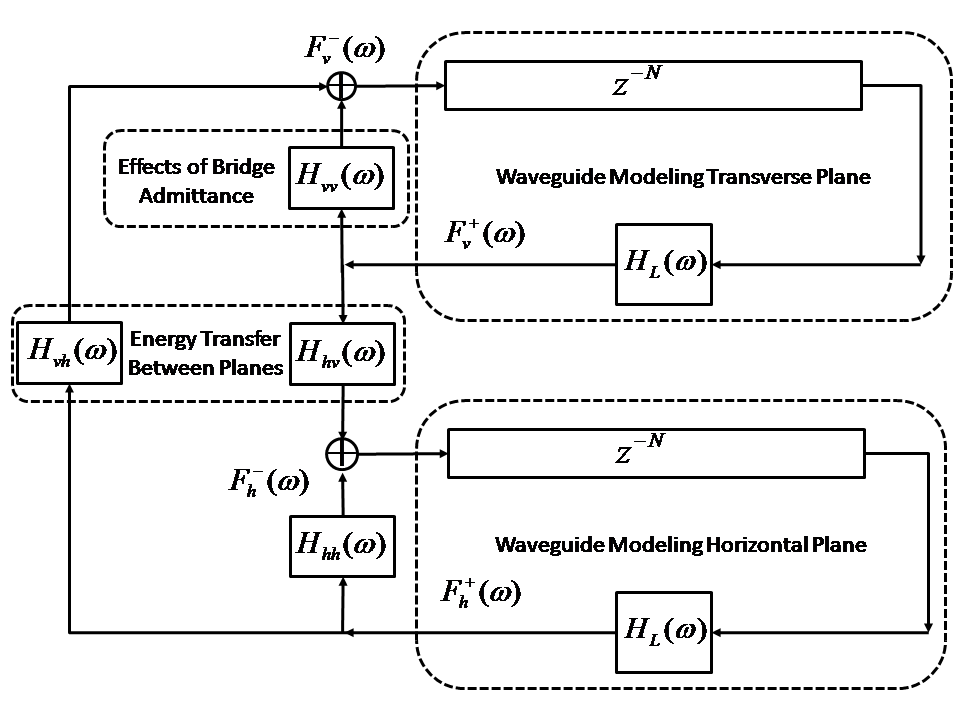Figure 15 shows the block diagram of two linearly coupled digital waveguides. One digital waveguide, denoted by the vertical direction corresponds to the direction of motion transverse to the instrument's body. The second digital waveguide, denoted by the horizontal direction corresponds to the direction of motion parallel to the instrument's body. Therefore, as a simplification, we often ignore the direct effects of the bridge on the horizontal plane of motion by not having $H_{hh}(\omega)$ in Figure 15.

Two-stage decay is clearly present in many stringed instruments. Though excitation is mechanically controlled in the piano, two-stage decay is also observed as the strings for a single note are carefully tuned to exhibit what is deemed psychoacoustically pleasing for the instrument. With two digital waveguides, each having different loop-filters for each digital waveguide, one can be set to decay at a faster rate than the other, such that the two-stage decay phenomenon is modeled. In Section 4.2.2, we discuss how to measure the decay of the string from different recordings and tune loop-filters to match the two different decay-rates.

Another phenomenon observed in physical instruments is initial pitch shifts that differ for each plane of vibration [10]. This phenomenon can be modeled using two digital waveguides per string with different time-varying lengths as discussed in Section 2.1.6.