Given a signal
![]() , its DFT is defined
by6.3
, its DFT is defined
by6.3
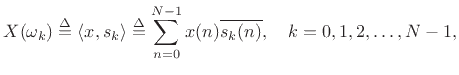
where
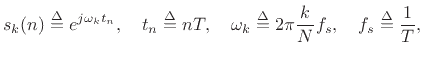
or, as it is most often written,
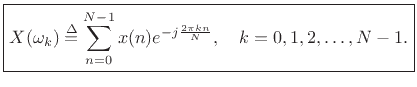
We may also refer to
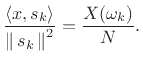
The projection of
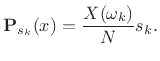
Since the
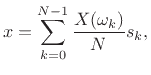
or, as we normally write,
In summary, the DFT is proportional to the set of coefficients of projection onto the sinusoidal basis set, and the inverse DFT is the reconstruction of the original signal as a superposition of its sinusoidal projections. This basic ``architecture'' extends to all linear orthogonal transforms, including wavelets, Fourier transforms, Fourier series, the discrete-time Fourier transform (DTFT), and certain short-time Fourier transforms (STFT). See Appendix B for some of these.
We have defined the DFT from a geometric signal theory point of view, building on the preceding chapter. See §7.1.1 for notation and terminology associated with the DFT.