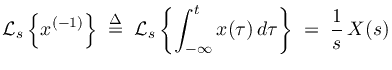Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The notion of a fractional derivative or integral is
naturally defined in terms of the integration and differentiation
theorems for Laplace/Fourier transforms. Let 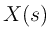 denote the
bilateral Laplace transform of
denote the
bilateral Laplace transform of 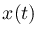 :
:
where
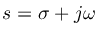 is a complex variable,
is a complex variable, 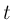 typically denotes
time in seconds, `
typically denotes
time in seconds, `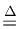 ' means ``equals by definition,'' and we
assume
' means ``equals by definition,'' and we
assume 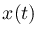 and all of its integrals and derivatives are absolutely
integrable and approach zero as
and all of its integrals and derivatives are absolutely
integrable and approach zero as
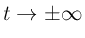 . Then the
differentiation theorem for bilateral Laplace transforms states
that
. Then the
differentiation theorem for bilateral Laplace transforms states
that
where
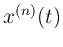 denotes the
denotes the 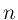 th derivative of
th derivative of 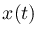 with respect
to
with respect
to 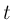 .2 The proof is quickly derived
using integration by parts.3
.2 The proof is quickly derived
using integration by parts.3
The integration theorem for Laplace transforms follows as a corollary:
The Laplace transform specializes to the Fourier transform along the
 axis in the complex plane, where
axis in the complex plane, where
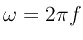 is
radian frequency (radians per second), while
is
radian frequency (radians per second), while 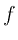 denotes
frequency in Hz (cycles per second).
denotes
frequency in Hz (cycles per second).
Subsections
Next |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download spectilt.pdf
[Comment on this page via email]
![]() denote the
bilateral Laplace transform of
denote the
bilateral Laplace transform of ![]() :
: