Filter Interpretation

As derived in obtaining Eq.(1) above, every fractional differintegral corresponds to a linear time-invariant filter having frequency-response

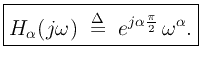$$\zbox{H_\alpha(j\omega) \isdefs e^{j\alpha\frac{\pi}{2}} \, \omega^\alpha.} \protect$$ (3)

Since this frequency response is not a rational polynomial in 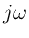$j\omega$ for non-integer $\alpha$ , there is no exact realization as a finite-order filter [#!JOSFP!#]. We must therefore settle for a finite-order approximation obtained using a truncated series expansion or filter design technique [#!ParksAndBurrus!#,#!JOST!#]. Many filter-design methods are available in the Matlab Filter Design Toolbox,¹⁰ and several basic design methods, such as invfreqz, are also available in the free, open-source, GNU Octave distribution.¹¹As far as we know, all filter-based approximations to date have been carried out along these lines.