Fractional Derivatives and Integrals

Since the $N$ th successive time derivative/integral of $x(t)$ Laplace-transforms to $s^{\pm N} X(s)$ , it follows that the fractional derivative of order $\alpha\in(0,1)$ , denoted by $x^{(\alpha)}$ , should correspond to the Laplace transform $s^\alpha X(s)$ , while the fractional integral of order $\alpha\in(0,1)$ corresponds to $s^{-\alpha} X(s)$ . We thus let $x^{(\alpha)}$ , $\alpha\in\mathbb{R}$ , denote both fractional integrals ($\alpha<0$ ) and derivatives ($\alpha>0$ ), possibly including both an integer and fractional part. However, since integer $\alpha=\pm N$ corresponds to a repeated ordinary derivative or integral, we will henceforth consider only $\alpha\in(-1,1)$ and implement any integer part in the usual way. Expressing $j$ as $e^{j\pi/2}$ so that $j^\alpha$ can be defined as $e^{j\alpha\pi/2}$ , we obtain the corresponding Laplace and Fourier transforms for fractional integration or differentiation as

$$\zbox{x^{(\alpha)}(t) \;\longleftrightarrow\;s^\alpha\, X(s) \;\;\stackrel{\longrightarrow}{{\scriptscriptstyle s=j\omega}}\;\; e^{j\alpha\frac{\pi}{2}}\, \omega^\alpha\, X(j\omega).} \protect$$ (1)

Thus, a fractional integral or derivative of order $\alpha$ corresponds to a phase shift by $\alpha \pi/2$ and a spectral ``tilt'' by $\omega^\alpha$ . For $\alpha=1$ , we obtain the frequency-response $j\omega$ of a differentiator, and for $\alpha=-1$ , the integrator frequency-response $-j/\omega$ is obtained, as required.

For integer $\alpha=N\in\mathbb{Z}$ , $N\ge 0$ , we have, from the convolution theorem for the unilateral Laplace transform applied to causal functions $x(t)$ ,⁴

$$s^{-N} X(s) \longleftrightarrow \frac{u(t)\,t^N}{(N-1)!} \ast x(t)$$

$$= \frac{1}{(N-1)!} \int_{0}^t x(\tau)\, (t-\tau)^{N-1} d\tau.\protect$$ (2)

where `$\ast$ ' denotes convolution, and $u(t)$ denotes the Heaviside unit step function:

$$u(t) \isdefs\left\{\begin{array}{ll} 1, & t\ge 0 \\ [5pt] 0, & t<0 \\ \end{array} \right.$$

This form was evidently developed originally as Cauchy's repeated integral formula.⁵

$$\begin{eqnarray*} x^{(-N)}(t) &\isdef& \int_a^{t} \int_a^{\tau_1} \cdots \int_a^{\tau_{N-1}} x(\tau_N) \,d\tau_N\,d\tau_{N-1}\,\cdots d\tau_1\\ [5pt] &=& \frac{1}{(N-1)!}\int_a^{t} (t-\tau)^{N-1} x(\tau)\, d\tau \end{eqnarray*}$$

where $a$ is any finite real number such that $x(t)=0,\,\forall t<a$ .

The generalization of $s^{-N}$ to $s^\alpha$ for $\alpha\in(-1,1)$ is quite natural. There is also no problem extending $(t-\tau)^{N-1}$ to $(t-\tau)^{-\alpha-1}$ in Eq.(2), and the lower limit of integration $a$ can be extended (for all practical purposes) as far as needed to the left to encompass the support of $x(t)$ . The last piece is generalizing $(N-1)!$ to $(-\alpha-1)!$ , which is provided by the gamma function⁶

$$\Gamma(t) \isdefs\int_0^\infty \tau^{t-1} e^{-\tau} d\tau$$

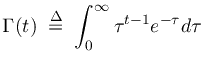
which, for positive integers $N$ , becomes $(N-1)$ factorial, i.e.,

$$\Gamma(N)=(N-1)!$$

for $N=1,2,3,\ldots\,$ . We thus obtain the expression for fractional integrodifferentiation in the time domain as the convolution integral

$$x^{(\alpha)}(t) \isdefs\frac{u(t)\,t^{-\alpha}}{\Gamma(-\alpha)} \ast x(t) \eqsp \frac{1}{\Gamma(-\alpha)} \int_0^t \frac{x(\tau)}{(t-\tau)^{\alpha+1}}d\tau.$$

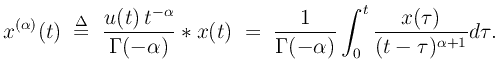
This is known as the Riemann-Liouville differintegral,⁷more commonly stated closer to the following form:

$$x^{(\alpha)}(t) = \frac{1}{\Gamma(-\alpha)} \int_a^t \frac{x(\tau)}{(t-\tau)^{\alpha+1}}d\tau.$$

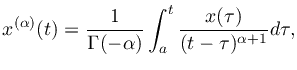
where $a$ is an arbitrary fixed base point, and $\alpha$ is any complex number with $\mbox{re\ensuremath{\left\{\alpha\right\}}}<0$ .⁸

The topic of fractional differentiation and integration falls within the well studied subject of fractional calculus⁹[#!OldhamAndSpanier74!#]. We will adopt the term ``differintegral'' from that literature.