Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Consider now applying a time varying modification.
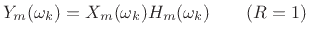 |
(10.32) |
where
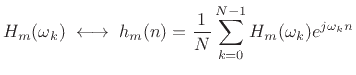 |
(10.33) |
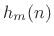 refers to the
refers to the  tap of the FIR filter at time
tap of the FIR filter at time 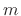 .
.
Hence, the result is the convolution of 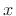 with the windowed
with the windowed 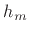 .
.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
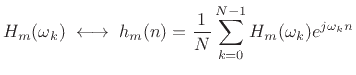
![\begin{eqnarray*}
y(m) &=& \frac{1}{N} \sum_{k=0}^{N-1} Y_m(\omega_k) e^{j\omega_k m} \\
&=& \frac{1}{N} \sum_{k=0}^{N-1} X_m(\omega_k)H_m(\omega_k) e^{j\omega_k m} \\
&=& \frac{1}{N} \sum_{k=0}^{N-1} \left\{ \sum_{n=-\infty}^\infty x(n)w(n-m)e^{-j\omega_kn} \right\} H_m(\omega_k) e^{j\omega_k m} \\
&=& \frac{1}{N} \sum_{n=-\infty}^\infty x(n)w(n-m) \sum_{k=0}^{N-1} H_m(\omega_k) e^{j\omega_k(m-n)} \\
&=& \sum_{n=-\infty}^\infty x(n) [ w(n-m) h_m(m-n)] \\
&=& \sum_{n=-\infty}^\infty x(n) [\tilde{w}(m-n)h_m(m-n)] \\
&=& (x*[\tilde{w} \cdot h_m])(m) \\
\end{eqnarray*}](img1701.png)
![]() with the windowed
with the windowed ![]() .
.