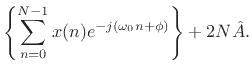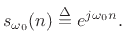Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Sinusoidal Amplitude Estimation
If the sinusoidal frequency  and phase
and phase 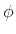 happen to be
known, we obtain a simple linear least squares problem for the
amplitude
happen to be
known, we obtain a simple linear least squares problem for the
amplitude 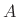 . That is, the error signal
. That is, the error signal
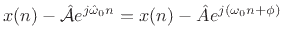 |
(6.36) |
becomes linear in the unknown parameter 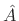 . As a result, the
sum of squared errors
. As a result, the
sum of squared errors
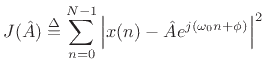 |
(6.37) |
becomes a simple quadratic (parabola) over the real
line.6.11 Quadratic forms in any number of
dimensions are easy to minimize. For example, the ``bottom of the
bowl'' can be reached in one step of Newton's method. From
another point of view, the optimal parameter 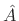 can be obtained as
the coefficient of orthogonal projection of the data
can be obtained as
the coefficient of orthogonal projection of the data 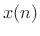 onto the space spanned by all values of
onto the space spanned by all values of 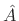 in the linear model
in the linear model
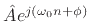 .
.
Yet a third way to minimize (5.37) is the method taught in
elementary calculus: differentiate
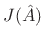 with respect to
with respect to 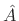 , equate
it to zero, and solve for
, equate
it to zero, and solve for 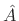 . In preparation for this, it is helpful to
write (5.37) as
. In preparation for this, it is helpful to
write (5.37) as
Differentiating with respect to 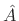 and equating to zero yields
and equating to zero yields
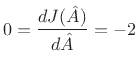 re re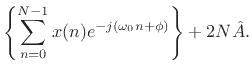 |
(6.38) |
Solving this for 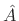 gives the optimal least-squares amplitude estimate
gives the optimal least-squares amplitude estimate
That is, the optimal least-squares amplitude estimate may be found by the
following steps:
- Multiply the data
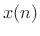 by
by
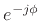 to zero the known phase
to zero the known phase 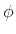 .
.
- Take the DFT of the
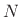 samples of
samples of 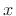 , suitably zero padded to approximate the DTFT, and evaluate it at the known frequency
, suitably zero padded to approximate the DTFT, and evaluate it at the known frequency  .
.
- Discard any imaginary part since it can only contain noise, by (5.39).
- Divide by
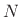 to obtain a properly normalized coefficient of projection
[264] onto the sinusoid
to obtain a properly normalized coefficient of projection
[264] onto the sinusoid
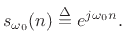 |
(6.40) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and phase
and phase ![]() happen to be
known, we obtain a simple linear least squares problem for the
amplitude
happen to be
known, we obtain a simple linear least squares problem for the
amplitude ![]() . That is, the error signal
. That is, the error signal
![]() with respect to
with respect to ![]() , equate
it to zero, and solve for
, equate
it to zero, and solve for ![]() . In preparation for this, it is helpful to
write (5.37) as
. In preparation for this, it is helpful to
write (5.37) as
![\begin{eqnarray*}
J({\hat A}) &\isdef & \sum_{n=0}^{N-1}
\left[x(n)-{\hat A}e^{j(\omega_0 n+\phi)}\right]
\left[\overline{x(n)}-\overline{{\hat A}} e^{-j(\omega_0 n+\phi)}\right]\\
&=&
\sum_{n=0}^{N-1}
\left[
\left\vert x(n)\right\vert^2
-
x(n)\overline{{\hat A}} e^{-j(\omega_0 n+\phi)}
-
\overline{x(n)}{\hat A}e^{j(\omega_0 n+\phi)}
+
{\hat A}^2
\right]
\\
&=& \left\Vert\,x\,\right\Vert _2^2 - 2\mbox{re}\left\{\sum_{n=0}^{N-1} x(n)\overline{{\hat A}}
e^{-j(\omega_0 n+\phi)}\right\}
+ N {\hat A}^2.
\end{eqnarray*}](img1040.png)
![]() and equating to zero yields
and equating to zero yields
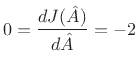 re
re