Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Sinusoidal Amplitude and Phase Estimation
The form of the optimal estimator (5.39) immediately suggests
the following generalization for the case of unknown amplitude and phase:
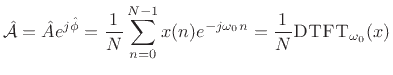 |
(6.41) |
That is,
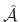 is given by the complex coefficient of
projection [264] of
is given by the complex coefficient of
projection [264] of 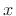 onto the complex sinusoid
onto the complex sinusoid
 at the known frequency
at the known frequency  . This can be shown by generalizing the
previous derivation, but here we will derive it using the more
enlightened orthogonality principle [114].
. This can be shown by generalizing the
previous derivation, but here we will derive it using the more
enlightened orthogonality principle [114].
The orthogonality principle for linear least squares estimation states
that the projection error must be orthogonal to the model.
That is, if 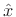 is our optimal signal model (viewed now as an
is our optimal signal model (viewed now as an
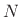 -vector in
-vector in
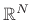 ), then we must have [264]
), then we must have [264]
Thus, the complex coefficient of projection of 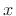 onto
onto
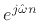 is given by
is given by
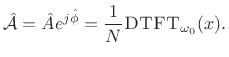 |
(6.42) |
The optimality of
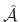 in the least squares sense follows from the
least-squares optimality of orthogonal projection
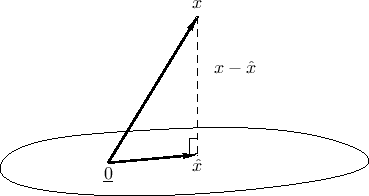
[114,121,252]. From a geometrical point of view,
referring to Fig.5.16, we say that the minimum distance from a
vector
in the least squares sense follows from the
least-squares optimality of orthogonal projection
[114,121,252]. From a geometrical point of view,
referring to Fig.5.16, we say that the minimum distance from a
vector
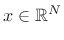 to some lower-dimensional subspace
to some lower-dimensional subspace
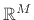 , where
, where
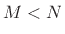 (here
(here  for one complex sinusoid) may be found by ``dropping
a perpendicular'' from
for one complex sinusoid) may be found by ``dropping
a perpendicular'' from 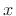 to the subspace. The point
to the subspace. The point 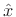 at the
foot of the perpendicular is the point within the subspace closest to
at the
foot of the perpendicular is the point within the subspace closest to
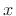 in Euclidean distance.
in Euclidean distance.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
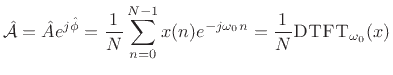
![]() is our optimal signal model (viewed now as an
is our optimal signal model (viewed now as an
![]() -vector in
-vector in
![]() ), then we must have [264]
), then we must have [264]
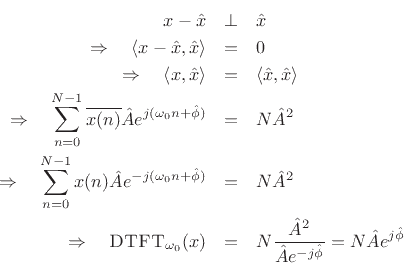
![]() onto
onto
![]() is given by
is given by