Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We define the shift operator for sampled signals 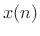 by
by
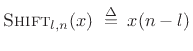 |
(3.18) |
where 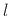 is any integer (
is any integer (
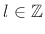 ). Thus,
). Thus,
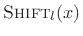 is a
right-shift or delay by
is a
right-shift or delay by 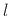 samples.
samples.
The shift theorem states3.5
 |
(3.19) |
or, in operator notation,
![$\displaystyle \hbox{\sc DTFT}_\omega[\hbox{\sc Shift}_l(x)] \eqsp \left( e^{-j\omega l} \right) X(\omega)$](img155.png) |
(3.20) |
Proof:
Note that
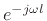 is a linear phase term, so called
because it is a linear function of frequency with slope equal to
is a linear phase term, so called
because it is a linear function of frequency with slope equal to 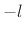 :
:
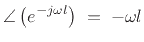 |
(3.21) |
The shift theorem gives us that multiplying a spectrum 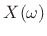 by
a linear phase term
by
a linear phase term
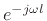 corresponds to a delay in
the time domain by
corresponds to a delay in
the time domain by 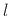 samples. If
samples. If 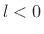 , it is called a time
advance by
, it is called a time
advance by 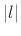 samples.
samples.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() by
by
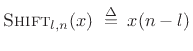

![\begin{eqnarray*}
\hbox{\sc DTFT}_\omega[\hbox{\sc Shift}_l(x)] &\isdef & \sum_{n=-\infty}^{\infty}x(n-l) e^{-j \omega n} \\
&=& \sum_{m=-\infty}^{\infty} x(m) e^{-j \omega (m+l)}
\qquad(m\isdef n-l) \\
&=& \sum_{m=-\infty}^{\infty}x(m) e^{-j \omega m} e^{-j \omega l} \\
&=& e^{-j \omega l} \sum_{m=-\infty}^{\infty}x(m) e^{-j \omega m} \\
&\isdef & e^{-j \omega l} X(\omega)
\end{eqnarray*}](img156.png)
![]() is a linear phase term, so called
because it is a linear function of frequency with slope equal to
is a linear phase term, so called
because it is a linear function of frequency with slope equal to ![]() :
: