Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Shift Operator
The shift operator is defined by
and
 denotes the entire shifted signal. Note that
since indexing is modulo
denotes the entire shifted signal. Note that
since indexing is modulo 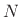 , the shift is circular (or
``cyclic''). However, we normally use it to represent time
delay by
, the shift is circular (or
``cyclic''). However, we normally use it to represent time
delay by  samples. We often use the shift operator in
conjunction with zero padding (appending zeros to the signal
samples. We often use the shift operator in
conjunction with zero padding (appending zeros to the signal
 , §7.2.7) in order to avoid the ``wrap-around''
associated with a circular shift.
, §7.2.7) in order to avoid the ``wrap-around''
associated with a circular shift.
Figure 7.2:
Successive one-sample shifts of a
sampled periodic sawtooth waveform having first period
![$ [0,1,2,3,4]$](img38.png) .
.
![\includegraphics[width=\twidth]{eps/shift}](img1146.png) |
Figure 7.2 illustrates successive one-sample delays of a periodic signal
having first period given by
![$ [0,1,2,3,4]$](img38.png) .
.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
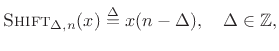
![\includegraphics[width=\twidth]{eps/shift}](img1146.png)
![]() .
.