Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Flip Operator
We define the flip operator by
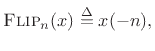 |
(7.1) |
for all sample indices
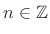 .
By modulo indexing,
.
By modulo indexing, 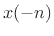 is the same as
is the same as 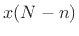 . The
. The
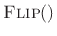 operator
reverses the order of samples
operator
reverses the order of samples 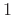 through
through  of a sequence, leaving
sample 0
alone, as shown in Fig.7.1a. Thanks to modulo
indexing, it can also be viewed as ``flipping'' the sequence about the
time 0, as shown in
Fig.7.1b. The interpretation of Fig.7.1b is usually the one we
want, and the
of a sequence, leaving
sample 0
alone, as shown in Fig.7.1a. Thanks to modulo
indexing, it can also be viewed as ``flipping'' the sequence about the
time 0, as shown in
Fig.7.1b. The interpretation of Fig.7.1b is usually the one we
want, and the
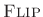 operator is usually thought of as ``time reversal''
when applied to a signal
operator is usually thought of as ``time reversal''
when applied to a signal 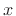 or ``frequency reversal'' when applied to a
spectrum
or ``frequency reversal'' when applied to a
spectrum 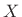 .
.
Figure 7.1:
Illustration of 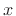 and
and
 for
for 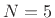 for the two main
domain conventions:
a)
for the two main
domain conventions:
a)
![$ n\in [0,N-1]$](img36.png) .
b)
.
b)
![$ n\in [-(N-1)/2, (N-1)/2]$](img37.png) .
.
![\includegraphics[width=\twidth]{eps/flip}](img1144.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]