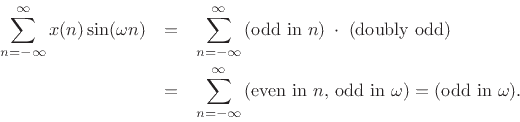![\begin{eqnarray*}
\hbox{\sc DTFT}_\omega(x)
& \isdef & \sum_{n=-\infty}^{\infty}x(n) e^{-j\omega n}\\
& = & \sum_{n=-\infty}^{\infty}x(n) \left[\cos(\omega n) + j\sin(\omega n)\right]\\
& = & \sum_{n=-\infty}^{\infty}x(n) \cos(\omega n) + j\sum_{n=-\infty}^{\infty}x(n)\sin(\omega n)\\
& = & \sum_{n=-\infty}^{\infty}x(n) \cos(\omega n)\\
& = & \hbox{real and even}
\end{eqnarray*}](img140.png)
If a signal is even in addition to being real, then its DTFT is also real and even. This follows immediately from the Hermitian symmetry of real signals, and the fact that the DTFT of any even signal is real:
![\begin{eqnarray*}
\hbox{\sc DTFT}_\omega(x)
& \isdef & \sum_{n=-\infty}^{\infty}x(n) e^{-j\omega n}\\
& = & \sum_{n=-\infty}^{\infty}x(n) \left[\cos(\omega n) + j\sin(\omega n)\right]\\
& = & \sum_{n=-\infty}^{\infty}x(n) \cos(\omega n) + j\sum_{n=-\infty}^{\infty}x(n)\sin(\omega n)\\
& = & \sum_{n=-\infty}^{\infty}x(n) \cos(\omega n)\\
& = & \hbox{real and even}
\end{eqnarray*}](img140.png)
This is true since cosine is even, sine is odd, even times even is even, even times odd is odd, and the sum over all samples of an odd signal is zero. I.e.,

and
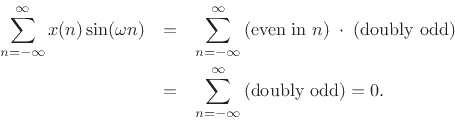
If ![]() is real and even, the following are true:
is real and even, the following are true:
![\begin{eqnarray*}
\hbox{\sc Flip}(x) & = & x \qquad \hbox{($x(-n)=x(n)$)}\\
\overline{x} & = & x\\ [5pt]
\hbox{\sc Flip}(X) & = & X\\
\overline{X} & = & X\\
\angle X(\omega) & =& 0 \hbox{ or } \pi
\end{eqnarray*}](img143.png)
Similarly, if a signal is odd and real, then its DTFT is odd and purely imaginary. This follows from Hermitian symmetry for real signals, and the fact that the DTFT of any odd signal is imaginary.
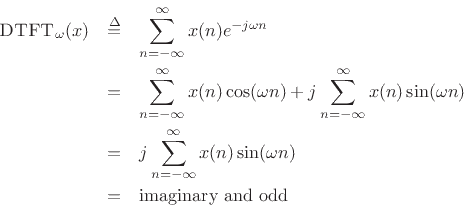
where we used the fact that
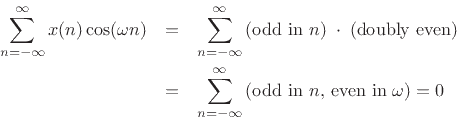
and