| (12.33) |
The well studied subject of Quadrature Mirror Filters (QMF) is entered by imposing the following symmetry constraint on the analysis filters:
In the time domain, the QMF constraint (11.33) becomes
![]() , i.e., all odd-index coefficients are negated. If
, i.e., all odd-index coefficients are negated. If ![]() is a lowpass filter cutting off near
is a lowpass filter cutting off near
![]() (as is typical),
then
(as is typical),
then ![]() is a complementary highpass filter. The exact cut-off
frequency can be adjusted along with the roll-off rate to provide a
maximally constant frequency-response sum.
is a complementary highpass filter. The exact cut-off
frequency can be adjusted along with the roll-off rate to provide a
maximally constant frequency-response sum.
Two-channel QMFs have been around since at least 1976 [51], and appear to be the first critically sampled perfect reconstruction filter banks. Moreover, the Princen-Bradley filter bank, the initial foundation of MPEG audio as we now know it, was conceived as the Fourier dual of QMFs [214]. Historically, the term QMF applied only to two-channel filter banks having the QMF symmetry constraint (11.33). Today, the term ``QMF filter bank'' may refer to more general PR filter banks with any number of channels and not obeying (11.33) [287].
Combining the QMF symmetry constraint with the aliasing-cancellation constraints, given by
![\begin{eqnarray*}
F_0(z) &=& \quad\! H_1(-z) \eqsp \quad\! H_0(z)\\ [5pt]
F_1(z) &=& -H_0(-z) \eqsp -H_1(z),
\end{eqnarray*}](img2047.png)
the perfect reconstruction requirement reduces to
It is easy to show using the polyphase representation of ![]() (see
[287]) that the only causal FIR QMF analysis filters yielding
exact perfect reconstruction are two-tap FIR filters of the
form
(see
[287]) that the only causal FIR QMF analysis filters yielding
exact perfect reconstruction are two-tap FIR filters of the
form
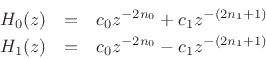
where ![]() and
and ![]() are constants, and
are constants, and ![]() and
and ![]() are integers.
Therefore, only weak channel filters are available in the QMF case
[
are integers.
Therefore, only weak channel filters are available in the QMF case
[
![]() ], as we saw in the amplitude-complementary case
above. On the other hand, very high quality IIR solutions are
possible. See [287, pp. 201-204] for details. In
practice, approximate ``pseudo QMF'' filters are more practical, which
only give approximate perfect reconstruction. We'll return to this
topic in §11.7.1.
], as we saw in the amplitude-complementary case
above. On the other hand, very high quality IIR solutions are
possible. See [287, pp. 201-204] for details. In
practice, approximate ``pseudo QMF'' filters are more practical, which
only give approximate perfect reconstruction. We'll return to this
topic in §11.7.1.
The scaled Haar filters, which we saw gave perfect reconstruction in the amplitude-complementary case, are also examples of a QMF filter bank:
![\begin{eqnarray*}
H_0(z) &=& 1 + z^{-1}\\ [5pt]
H_1(z) &=& 1 - z^{-1}
\end{eqnarray*}](img2055.png)
In this example, ![]() , and
, and ![]() .
.