![\includegraphics[width=0.7\twidth]{eps/dyadicFilters}](img2364.png) |
A dyadic filter bank is any octave filter
bank,12.6 as illustrated qualitatively in Figure 11.34. Note that
![]() is the top-octave bandpass filter,
is the top-octave bandpass filter,
![]() is the bandpass filter for next octave down,
is the bandpass filter for next octave down,
![]() is the octave bandpass below that, and so on. The optional
scale factors result in the same sum-of-squares for each
channel-filter impulse response.
is the octave bandpass below that, and so on. The optional
scale factors result in the same sum-of-squares for each
channel-filter impulse response.
A dyadic filter bank may be derived from the discrete wavelet filter
bank by setting ![]() and relaxing the exact orthonormality
requirement on the channel-filter impulse responses. If they do
happen to be orthonormal, we may call it a dyadic wavelet filter
bank.
and relaxing the exact orthonormality
requirement on the channel-filter impulse responses. If they do
happen to be orthonormal, we may call it a dyadic wavelet filter
bank.
For a dyadic filter bank, the center-frequency of the ![]() th
channel-filter impulse response can be defined as
th
channel-filter impulse response can be defined as
| (12.123) |
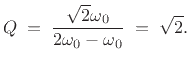 |
(12.124) |