![\begin{psfrags}
% latex2html id marker 30517\psfrag{x(n)}{\normalsize $x(n)$}\psfrag{x}{\normalsize $x$}\psfrag{(n)}{\normalsize $(n)$}\psfrag{y}{\normalsize $y$}\psfrag{v}{\normalsize $v$}\psfrag{H}{\normalsize $H$}\psfrag{F}{\normalsize $F$}\psfrag{z}{\normalsize $z$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/cqfcopy}
\caption{Two-channel polyphase filter bank and inverse.}
\end{figure}
\end{psfrags}](img2034.png)
Let's look at the polyphase representation for this example. Starting
with the filter bank and its reconstruction (see Fig.11.17), the
polyphase decomposition of ![]() is
is
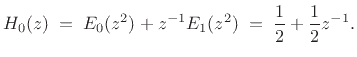 |
(12.31) |
| (12.32) |
![\begin{eqnarray*}
\hat{X}(z) &=& \left[F_0(z)H_0(z) + F_1(z)H_1(z)\right] X(z)\\
&=& \left[\left(\frac{1}{2} + \frac{1}{2}z^{-1}\right)H_0(z) + \left(-\frac{1}{2}+\frac{1}{2}z^{-1}\right)H_1(z)\right]X(z)\\
&=& \frac{1}{2}\left\{\left[H_0(z)-H_1(z)\right] + z^{-1}\left[H_0(z) + H_1(z)\right]\right\}X(z)
\end{eqnarray*}](img2038.png)
The polyphase representation of the filter bank and its reconstruction can now be drawn as in Fig.11.18. Notice that the reconstruction filter bank is formally the transpose of the analysis filter bank [263]. A filter bank that is inverted by its own transpose is said to be an orthogonal filter bank, a subject to which we will return §11.3.8.
![\includegraphics[width=\twidth]{eps/poly2chan}](img2039.png) |
Commuting the downsamplers (using the noble identities from
§11.2.5), we obtain Figure 11.19. Since
![]() , this is simply the OLA form of an
STFT filter bank for
, this is simply the OLA form of an
STFT filter bank for ![]() , with
, with ![]() , and rectangular
window
, and rectangular
window
![]() . That is, the DFT size, window length, and hop
size are all 2, and both the DFT and its inverse are simply
sum-and-difference operations.
. That is, the DFT size, window length, and hop
size are all 2, and both the DFT and its inverse are simply
sum-and-difference operations.