The periodogram is based on the definition of the power
spectral density (PSD) (see Appendix C). Let
![]() denote a windowed segment of samples from a random process
denote a windowed segment of samples from a random process ![]() ,
where the window function
,
where the window function ![]() (classically the rectangular window)
contains
(classically the rectangular window)
contains ![]() nonzero samples. Then the periodogram is defined as the
squared-magnitude DTFT of
nonzero samples. Then the periodogram is defined as the
squared-magnitude DTFT of ![]() divided by
divided by ![]() [120, p. 65]:7.7
[120, p. 65]:7.7
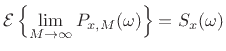 |
(7.24) |
In terms of the sample PSD defined in §6.7, we have
| (7.25) |
In practice, we of course compute a sampled periodogram
![]() ,
,
![]() , replacing the DTFT with the
length
, replacing the DTFT with the
length ![]() FFT. Essentially, the steps of §6.9
include computation of the periodogram.
FFT. Essentially, the steps of §6.9
include computation of the periodogram.
As mentioned in §6.9, a problem with the periodogram of noise
signals is that it too is random for most purposes. That is,
while the noise has been split into bands by a Fourier transform, it
has not been averaged in any way that reduces randomness within each band, and each
band produces a nearly independent random value. In fact, it can be
shown [120] that
![]() is a random variable whose
standard deviation (square root of its variance) is comparable to its
mean. This is not a measure of noise level in each band.
is a random variable whose
standard deviation (square root of its variance) is comparable to its
mean. This is not a measure of noise level in each band.
The trick to noise spectrum analysis is that many sample power spectra (squared-magnitude FFTs) must be averaged to obtain a ``stable'' statistical estimate of the noise spectral envelope. This is the essence of Welch's method for spectrum analysis of stochastic processes, as elaborated in §6.12 below. The right column of Fig.6.1 illustrates the effect of this averaging for white noise.