Bartlett (``Triangular'') Window

The Bartlett window (or simply triangular window) may be defined by

$$w(n) = w_R(n)\left[1 - \frac{\vert n\vert}{\frac{M-1}{2}}\right], \quad n\in\left[-\frac{M-1}{2},\frac{M-1}{2}\right]$$ (4.31)

and the corresponding transform is

$$W(\omega) = \left(\frac{M-1}{2}\right)^2\hbox{asinc}_{\frac{M-1}{2}}^2(\omega)$$ (4.32)

The following properties are immediate:

• Convolution of two length 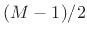$(M-1)/2$ rectangular windows
• Main lobe twice as wide as that of a rectangular window of length $M$
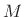
• First side lobe twice as far down as rectangular case (-26 dB)
• Often applied implicitly to sample correlations of finite data
• Also called the ``tent function''
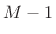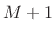• Can replace $M-1$ by $M+1$ to avoid including endpoint zeros