Definition: The expected value of a continuous random variable
Definition:
The expected value of a continuous random variable
![]() is denoted
is denoted ![]() and is defined by
and is defined by
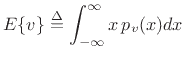 |
(C.12) |
Example:
Let the random variable ![]() be uniformly distributed between
be uniformly distributed between
![]() and
and ![]() , i.e.,
, i.e.,
![$\displaystyle p_v(x) = \left\{\begin{array}{ll} \frac{1}{b-a}, & a\leq x \leq b \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$](img2636.png) |
(C.13) |
 |
(C.14) |
For a stochastic process, which is simply a sequence of random
variables, ![]() means the expected value of
means the expected value of ![]() over
``all realizations'' of the random process
over
``all realizations'' of the random process ![]() . This is also
called an ensemble average. In other words, for each ``roll of
the dice,'' we obtain an entire signal
. This is also
called an ensemble average. In other words, for each ``roll of
the dice,'' we obtain an entire signal
![]() , and to compute
, and to compute ![]() , say, we average
together all of the values of
, say, we average
together all of the values of ![]() obtained for all ``dice rolls.''
obtained for all ``dice rolls.''
For a stationary random process
![]() , the random variables
, the random variables ![]() which make it up
are identically distributed. As a result, we may normally compute
expected values by averaging over time within a single
realization of the random process, instead of having to average
``vertically'' at a single time instant over many realizations of the
random process.C.2 Denote time averaging by
which make it up
are identically distributed. As a result, we may normally compute
expected values by averaging over time within a single
realization of the random process, instead of having to average
``vertically'' at a single time instant over many realizations of the
random process.C.2 Denote time averaging by
 |
(C.15) |
We are concerned only with stationary stochastic processes in this book. While the statistics of noise-like signals must be allowed to evolve over time in high quality spectral models, we may require essentially time-invariant statistics within a single frame of data in the time domain. In practice, we choose our spectrum analysis window short enough to impose this. For audio work, 20 ms is a typical choice for a frequency-independent frame length.C.3 In a multiresolution system, in which the frame length can vary across frequency bands, several periods of the band center-frequency is a reasonable choice. As discussed in §5.5.2, the minimum number of periods required under the window for resolution of spectral peaks depends on the window type used.