Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Practical Bottom Line
Since we must use the DFT in practice, preferring an FFT for speed,
we typically compute the sample autocorrelation function for a
length  sequence
sequence 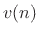 ,
,
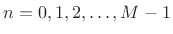 as follows:
as follows:
- Choose the FFT size
 to be a power of 2
providing at least
to be a power of 2
providing at least 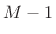 samples of zero padding
(
samples of zero padding
(
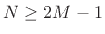 ):
):
![$\displaystyle x \isdef [v(0),v(1),\ldots,v(M-1), \underbrace{0,\ldots,0}_{\hbox{$N-M$}}].$](img1141.png) |
(7.21) |
- Perform a length
 FFT to get
FFT to get
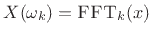 .
.
- Compute the squared magnitude
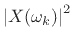 .
.
- Compute the inverse FFT to get
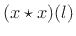 ,
,
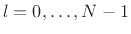 .
.
- Remove the bias, if desired, by dividing out the implicit
Bartlett-window weighting to get
![$\displaystyle \hat{r}_{v,M}(l) \isdef \left\{\begin{array}{ll} \frac{1}{M-\vert l\vert} (x\star x)(l), & l=0,\,\pm1,\,\pm2,\,\pm (M-1)\;\mbox{(mod $N$)} \\ [5pt] 0, & \vert l\vert\geq M\; \mbox{(mod $N$)}. \\ \end{array} \right.$](img1146.png) |
(7.22) |
Often the sample mean (average value) of the  samples of
samples of 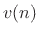 is
removed prior to taking an FFT. Some implementations also
detrend the data, which means removing any linear ``tilt'' in
the data.7.6
is
removed prior to taking an FFT. Some implementations also
detrend the data, which means removing any linear ``tilt'' in
the data.7.6
It is important to note that the sample autocorrelation is itself a
stochastic process. To stably estimate a true autocorrelation
function, or its Fourier transform the power spectral density, many
sample autocorrelations (or squared-magnitude FFTs) must be
averaged together, as discussed in §6.12 below.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() sequence
sequence ![]() ,
,
![]() as follows:
as follows:
![$\displaystyle x \isdef [v(0),v(1),\ldots,v(M-1), \underbrace{0,\ldots,0}_{\hbox{$N-M$}}].$](img1141.png)
![$\displaystyle \hat{r}_{v,M}(l) \isdef \left\{\begin{array}{ll} \frac{1}{M-\vert l\vert} (x\star x)(l), & l=0,\,\pm1,\,\pm2,\,\pm (M-1)\;\mbox{(mod $N$)} \\ [5pt] 0, & \vert l\vert\geq M\; \mbox{(mod $N$)}. \\ \end{array} \right.$](img1146.png)