Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The Gaussian is infinitely flat at infinity. Equivalently, the
Maclaurin expansion (Taylor expansion about 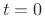 ) of
) of
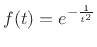 |
(D.3) |
is zero for all orders. Thus, even though 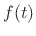 is
differentiable of all orders at
is
differentiable of all orders at 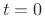 , its series expansion fails to
approach the function. This happens because
, its series expansion fails to
approach the function. This happens because 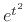 has an
essential singularity at
has an
essential singularity at 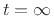 (also called a
``non-removable singularity''). One can think of an essential
singularity as an infinite number of poles piled up at the same
point (
(also called a
``non-removable singularity''). One can think of an essential
singularity as an infinite number of poles piled up at the same
point (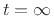 for
for 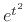 ). Equivalently,
). Equivalently, 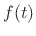 above has an
infinite number of zeros at
above has an
infinite number of zeros at 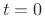 , leading to the problem with
Maclaurin series expansion. To prove this, one can show
, leading to the problem with
Maclaurin series expansion. To prove this, one can show
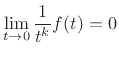 |
(D.4) |
for all
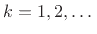 . This follows from the fact that exponential
growth or decay is faster than polynomial growth or decay. An
exponential can in fact be viewed as an infinite-order polynomial,
since
. This follows from the fact that exponential
growth or decay is faster than polynomial growth or decay. An
exponential can in fact be viewed as an infinite-order polynomial,
since
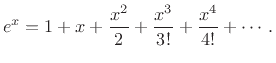 |
(D.5) |
We may call
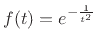 infinitely flat at
infinitely flat at
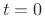 in the ``Padé sense'':
in the ``Padé sense'':
Another interesting mathematical property of essential singularities is
that near an essential singular point
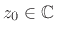 the
inequality
the
inequality
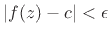 |
(D.6) |
is satisfied at some point 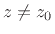 in every neighborhood of
in every neighborhood of
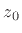 , however small. In other words,
, however small. In other words,  comes arbitrarily close
to every possible value in any neighborhood about an
essential singular point. This was first proved by Weierstrass
[42, p. 270].
comes arbitrarily close
to every possible value in any neighborhood about an
essential singular point. This was first proved by Weierstrass
[42, p. 270].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ) of
) of
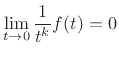
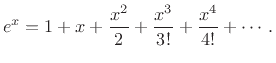
![]() the
inequality
the
inequality