Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We have a function  and we want to approximate it using an
and we want to approximate it using an
 th-order polynomial:
th-order polynomial:
where
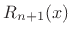 , the approximation error, is called the
remainder term. We may
assume
, the approximation error, is called the
remainder term. We may
assume  and
and  are real, but the following derivation
generalizes unchanged to the complex case.
are real, but the following derivation
generalizes unchanged to the complex case.
Our problem is to find fixed constants
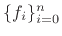 so as to obtain
the best approximation possible. Let's proceed optimistically as though
the approximation will be perfect, and assume
so as to obtain
the best approximation possible. Let's proceed optimistically as though
the approximation will be perfect, and assume
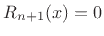 for all
for all 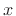 (
(
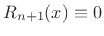 ), given the right values of
), given the right values of 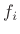 . Then at
. Then at 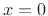 we
must have
we
must have
That's one constant down and  to go! Now let's look at the first
derivative of
to go! Now let's look at the first
derivative of  with respect to
with respect to 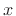 , again assuming that
, again assuming that
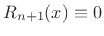 :
:
Evaluating this at 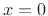 gives
gives
In the same way, we find
where
 denotes the
denotes the  th derivative of
th derivative of  with respect to
with respect to
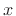 , evaluated at
, evaluated at 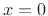 . Solving the above relations for the desired
constants yields
. Solving the above relations for the desired
constants yields
Thus, defining
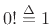 (as it always is), we have derived the
following polynomial approximation:
(as it always is), we have derived the
following polynomial approximation:
This is the  th-order Taylor series expansion of
th-order Taylor series expansion of  about the
point
about the
point 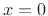 . Its derivation was quite simple. The hard part is
showing that the approximation error (remainder term
. Its derivation was quite simple. The hard part is
showing that the approximation error (remainder term
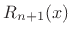 ) is
small over a wide interval of
) is
small over a wide interval of 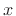 values. Another ``math job'' is to
determine the conditions under which the approximation error
approaches zero for all
values. Another ``math job'' is to
determine the conditions under which the approximation error
approaches zero for all 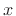 as the order
as the order  goes to infinity. The
main point to note here is that the Taylor series itself is simple to
derive.
goes to infinity. The
main point to note here is that the Taylor series itself is simple to
derive.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and we want to approximate it using an
and we want to approximate it using an
![]() th-order polynomial:
th-order polynomial:
![]() so as to obtain
the best approximation possible. Let's proceed optimistically as though
the approximation will be perfect, and assume
so as to obtain
the best approximation possible. Let's proceed optimistically as though
the approximation will be perfect, and assume
![]() for all
for all ![]() (
(
![]() ), given the right values of
), given the right values of ![]() . Then at
. Then at ![]() we
must have
we
must have
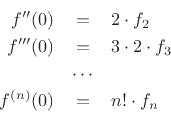
![]() denotes the
denotes the ![]() th derivative of
th derivative of ![]() with respect to
with respect to
![]() , evaluated at
, evaluated at ![]() . Solving the above relations for the desired
constants yields
. Solving the above relations for the desired
constants yields

![]() (as it always is), we have derived the
following polynomial approximation:
(as it always is), we have derived the
following polynomial approximation:
