Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The Hilbert transform 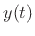 of a real, continuous-time signal
of a real, continuous-time signal
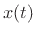 may be expressed as the convolution of
may be expressed as the convolution of  with the
Hilbert transform kernel:
with the
Hilbert transform kernel:
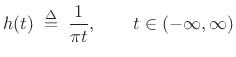 |
(5.17) |
That is, the Hilbert transform of 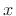 is given by
is given by
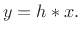 |
(5.18) |
Thus, the Hilbert transform is a non-causal linear time-invariant filter.
The complex analytic signal 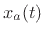 corresponding to the real signal
corresponding to the real signal 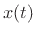 is
then given by
is
then given by
To show this last equality (note the lower limit of 0
instead of the
usual 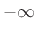 ), it is easiest to apply (4.16) in the frequency
domain:
), it is easiest to apply (4.16) in the frequency
domain:
Thus, the negative-frequency components of 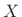 are canceled, while the
positive-frequency components are doubled. This occurs because, as
discussed above, the Hilbert transform is an allpass filter that
provides a
are canceled, while the
positive-frequency components are doubled. This occurs because, as
discussed above, the Hilbert transform is an allpass filter that
provides a 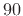 degree phase shift at all negative frequencies, and a
degree phase shift at all negative frequencies, and a
 degree phase shift at all positive frequencies, as indicated in
(4.16). The use of the Hilbert transform to create an analytic
signal from a real signal is one of its main applications. However,
as the preceding sections make clear, a Hilbert transform in practice
is far from ideal because it must be made finite-duration in some way.
degree phase shift at all positive frequencies, as indicated in
(4.16). The use of the Hilbert transform to create an analytic
signal from a real signal is one of its main applications. However,
as the preceding sections make clear, a Hilbert transform in practice
is far from ideal because it must be made finite-duration in some way.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() of a real, continuous-time signal
of a real, continuous-time signal
![]() may be expressed as the convolution of
may be expressed as the convolution of ![]() with the
Hilbert transform kernel:
with the
Hilbert transform kernel:
![]() corresponding to the real signal
corresponding to the real signal ![]() is
then given by
is
then given by
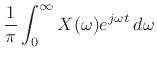
![]() ), it is easiest to apply (4.16) in the frequency
domain:
), it is easiest to apply (4.16) in the frequency
domain: