Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We need a Hilbert-transform filter 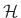 to compute the imaginary
part
to compute the imaginary
part 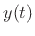 of the analytic signal
of the analytic signal 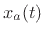 given its real part
given its real part
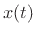 . That is,
. That is,
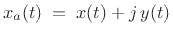 |
(5.14) |
where
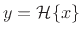 . In the frequency domain, we have
. In the frequency domain, we have
![$\displaystyle X_a(\omega) \eqsp X(\omega) + j\,Y(\omega) \eqsp \left[1+j\,H(\omega)\right]\,X(\omega)$](img745.png) |
(5.15) |
where 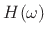 denotes the frequency response of the Hilbert
transform
denotes the frequency response of the Hilbert
transform 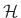 . Since by definition we have
. Since by definition we have
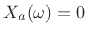 for
for
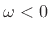 , we must have
, we must have
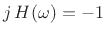 for
for 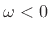 , so that
, so that
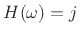 for negative frequencies (an allpass response with
phase-shift
for negative frequencies (an allpass response with
phase-shift 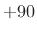 degrees). To pass the positive-frequency components
unchanged, we would most naturally define
degrees). To pass the positive-frequency components
unchanged, we would most naturally define
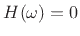 for
for
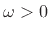 . However, conventionally, the positive-frequency
Hilbert-transform frequency response is defined more symmetrically as
. However, conventionally, the positive-frequency
Hilbert-transform frequency response is defined more symmetrically as
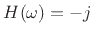 for
for 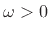 , which gives
, which gives
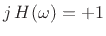 and
and
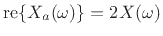 , i.e., the positive-frequency
components of
, i.e., the positive-frequency
components of 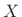 are multiplied by
are multiplied by  .
.
In view of the foregoing, the frequency response of the ideal
Hilbert-transform filter may be defined as follows:
![$\displaystyle H(\omega) \isdefs \left\{\begin{array}{ll} \quad\! j, & \omega<0 \\ [5pt] \quad\!0, & \omega=0 \\ [5pt] -j, & \omega>0 \\ \end{array} \right. \protect$](img757.png) |
(5.16) |
Note that the point at 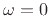 can be defined arbitrarily since the
inverse-Fourier transform integral is not affected by a single finite
point (being a ``set of measure zero'').
can be defined arbitrarily since the
inverse-Fourier transform integral is not affected by a single finite
point (being a ``set of measure zero'').
The ideal filter impulse response 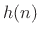 is obtained by finding the
inverse Fourier transform of (4.16). For discrete time, we may
take the inverse DTFT of (4.16) to obtain the ideal discrete-time
Hilbert-transform impulse response, as pursued in Problem 10.
We will work with the usual continuous-time limit
is obtained by finding the
inverse Fourier transform of (4.16). For discrete time, we may
take the inverse DTFT of (4.16) to obtain the ideal discrete-time
Hilbert-transform impulse response, as pursued in Problem 10.
We will work with the usual continuous-time limit
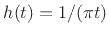 in
the next section.
in
the next section.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() to compute the imaginary
part
to compute the imaginary
part ![]() of the analytic signal
of the analytic signal ![]() given its real part
given its real part
![]() . That is,
. That is,
![]() is obtained by finding the
inverse Fourier transform of (4.16). For discrete time, we may
take the inverse DTFT of (4.16) to obtain the ideal discrete-time
Hilbert-transform impulse response, as pursued in Problem 10.
We will work with the usual continuous-time limit
is obtained by finding the
inverse Fourier transform of (4.16). For discrete time, we may
take the inverse DTFT of (4.16) to obtain the ideal discrete-time
Hilbert-transform impulse response, as pursued in Problem 10.
We will work with the usual continuous-time limit
![]() in
the next section.
in
the next section.