Filtering and Downsampling

Because downsampling by $N$ causes aliasing of any frequencies in the original signal above $\vert\omega\vert > \pi/N$ , the input signal may need to be first lowpass-filtered to prevent this aliasing, as shown in Fig.11.5.

Figure 11.5: Lowpass filtering followed by downsampling.

Suppose we implement such an anti-aliasing lowpass filter $h(n)$ as an FIR filter of length $M\le N$ with cut-off frequency $\pi/N$ .^12.1 This is drawn in direct form in Fig.11.6.

Figure 11.6: Direct-form implementation of an FIR anti-aliasing lowpass filter followed by a downsampler.

Figure 11.7: FIR lowpass filter with downsampler commuted inside the direct-form filter.

We do not need $N-1$ out of every $N$ filter output samples due to the $N$ :$1$ downsampler. To realize this savings, we can commute the downsampler through the adders inside the FIR filter to obtain the result shown in Fig.11.7. The multipliers are now running at $1/N$ times the sampling frequency of the input signal $x(n)$ . This reduces the computation requirements by a factor of $1/N$ . The downsampler outputs in Fig.11.7 are called polyphase signals. The overall system is a summed polyphase filter bank in which each ``subphase filter'' is a constant scale factor $h(m)$ . As we will see, more general subphase filters can be used to implement time-domain aliasing as needed for Portnoff windows (§9.7).

We may describe the polyphase processing in the anti-aliasing filter of Fig.11.7 as follows:

• Subphase signal 0

  $$x(nN)\left\vert _{n=0}^{\infty}\right. \eqsp [x_0,x_N,x_{2N},\ldots]$$ (12.3)

  
  
  is scaled by $h(0)$ .

• Subphase signal 1

  $$x(nN-1)\left\vert _{n=0}^{\infty}\right.\eqsp [x_{-1},x_{N-1},x_{2N-1},\ldots]$$ (12.4)

  
  
  is scaled by $h(1)$ ,

• $\cdots$

• Subphase signal $M-1$
  $$x(nN-m)\left\vert _{n=0}^{\infty}\right.\eqsp [x_{-m},x_{N-m},x_{2N-m},\ldots]$$
  is scaled by $h(M-1)$ .

These scaled subphase signals are finally summed to form the output signal shown in Fig.11.7

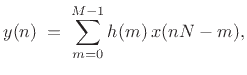$$y(n) \eqsp \sum_{m=0}^{M-1} h(m)\, x(nN-m),$$ (12.5)

which we recognize as a direct-form-convolution implementation of a length $M$ FIR filter $h$ , with its output downsampled by the factor $N$ .

The summed polyphase signals of Fig.11.7 can be interpreted as ``serial to parallel conversion'' from an ``interleaved'' stream of scalar samples $x(n)$ to a ``deinterleaved'' sequence of buffers (each length $M$ ) every $N$ samples, followed by an inner product of each buffer with $h = [h(0),\ldots,h(M-1)]$ . The same operation may be visualized as a deinterleaving through variable gains into a running sum, as shown in Fig.11.8.

Figure 11.8: Demultiplex-and-sum interpretation of the polyphase signal sum of Fig.11.7.