For sequences of length ![]() , the cyclic autocorrelation operator is defined by
, the cyclic autocorrelation operator is defined by
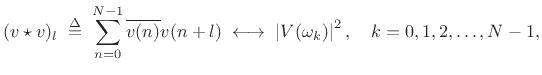 |
(7.19) |
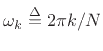 and the index
and the index By using zero padding by a factor of 2 or more, cyclic autocorrelation also implements acyclic autocorrelation as defined in (6.16).
An unbiased cyclic autocorrelation is obtained, in the
zero-mean case, by simply normalizing ![]() by the number
of terms in the sum:
by the number
of terms in the sum:
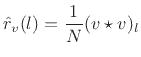 |
(7.20) |