Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The sample autocorrelation defined in (6.6) is not quite
the same as the autocorrelation function for infinitely long
discrete-time sequences defined in §2.3.6,
viz.,
where the signal 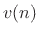 is assumed to be of finite support
(nonzero over a finite range of samples), and
is assumed to be of finite support
(nonzero over a finite range of samples), and 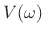 is the DTFT
of
is the DTFT
of  . The advantage of the definition of
. The advantage of the definition of 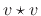 is that
there is a simple
Fourier theorem associated with it. The disadvantage is that
it is biased as an estimate of the statistical autocorrelation.
The bias can be removed, however, since
is that
there is a simple
Fourier theorem associated with it. The disadvantage is that
it is biased as an estimate of the statistical autocorrelation.
The bias can be removed, however, since
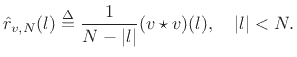 |
(7.15) |
Thus, 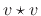 can be seen as a Bartlett-windowed sample
autocorrelation:
can be seen as a Bartlett-windowed sample
autocorrelation:
![$\displaystyle (v\star v)(l) = \left\{\begin{array}{ll} (N-\left\vert l\right\vert) \hat{r}_{v,N}(l), & l=0,\pm1,\pm2,\ldots,\pm (N-1) \\ [5pt] 0, & \vert l\vert\geq N. \\ \end{array} \right. \protect$](img1130.png) |
(7.16) |
It is common in practice to retain the implicit Bartlett
(triangular) weighting in the sample autocorrelation. It merely
corresponds to smoothing of the power spectrum (or
cross-spectrum) with the
 kernel, and smoothing is necessary
anyway for statistical stability. It also down-weights the less
reliable large-lag estimates, weighting each lag by the number of
lagged products that were summed, which seems natural.
kernel, and smoothing is necessary
anyway for statistical stability. It also down-weights the less
reliable large-lag estimates, weighting each lag by the number of
lagged products that were summed, which seems natural.
The left column of Fig.6.1 in fact shows the Bartlett-biased
sample autocorrelation. When the bias is removed, the autocorrelation
appears noisier at higher lags (near the endpoints of the plot).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]