Convolving with Long Signals

We saw that we can perform efficient convolution of two finite-length sequences using a Fast Fourier Transform (FFT). There are some situations, however, in which it is impractical to use a single FFT for each convolution operand:

• One or both of the signals being convolved is very long.
• The filter must operate in real time. (We can't wait until the input signal ends before providing an output signal.)

Direct convolution does not have these problems. For example, given a causal finite-impulse response (FIR) $h$ of length $L$ , we need only store the past $L-1$ samples of the input signal $x$ to calculate the next output sample, since

$$\begin{eqnarray*} y(n) &=& (h\ast x)(n) = \sum_{m=0}^n h(m)x(n-m)\\ &=& h(0)x(n) + h(1)x(n-1) +\cdots+ h(L-1) x(n-L+1) \end{eqnarray*}$$

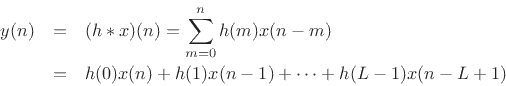
Thus, at every time $n$ , the output $y(n)$ can be computed as a linear combination of the current input sample $x(n)$ and the current filter state $\{x(n-1),\ldots,x(n-L+1)\}$ .

To obtain the benefit of high-speed FFT convolution when the input signal is very long, we simply chop up the input signal $x$ into blocks, and perform convolution on each block separately. The output is then the sum of the separately filtered blocks. The blocks overlap because of the ``ringing'' of the filter. For a zero-phase filter, each block overlaps with both of its neighboring blocks. For causal filters, each block overlaps only with its neighbor to the right (the next block in time). The fact that signal blocks overlap and must be added together (instead of simply abutted) is the source of the name overlap-add method for FFT convolution of long sequences [7,9].

The idea of processing input blocks separately can be extended also to both operands of a convolution (both $x$ and $h$ in $x\ast h$ ). The details are a straightforward extension of the single-block-signal case discussed below.

When simple FFT convolution is being performed between a signal $x$ and FIR filter $h$ , there is no reason to use a non-rectangular window function on each input block. A rectangular window length of $M$ samples may advance $M$ samples for each successive frame (hop size $=M$ samples). In this case, the input blocks do not overlap, while the output blocks overlap by the FIR filter length (minus one sample). On the other hand, if nonlinear and/or time-varying spectral modifications to be performed, then there are good reasons to use a non-rectangular window function and a smaller hop size, as we will develop below.