Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
To represent practical FFT implementations, it is preferable
to shift the 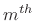 frame back to the time origin:
frame back to the time origin:
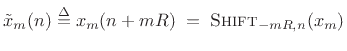 |
(9.20) |
This is summarized in Fig.8.11. Zero-based frames are needed
because the leftmost input sample is assigned to time zero by FFT algorithms.
In other words, a hopping FFT effectively redefines
time zero on each hop. Thus, a practical STFT is a sequence of FFTs
of the zero-based frames
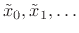 . On the other hand,
papers in the literature (such as [7,9]) work with the fixed time-origin case (
. On the other hand,
papers in the literature (such as [7,9]) work with the fixed time-origin case (
 ). Since they differ only by a time shift, it is not hard to
translate back and forth.
). Since they differ only by a time shift, it is not hard to
translate back and forth.
![\begin{psfrags}
% latex2html id marker 22379\psfrag{x}{$x$}\psfrag{Zero-centered 3rd frame x_3: M = 64, R = M/2}%
{\normalsize Zero-centered 3rd frame $x_3$: $M = 64$, $R = M/2$}\psfrag{x_3}{$x_3$} % doesn't work\psfrag{xtilde_3}{${\tilde x}_3$}\begin{figure}[htbp]
\includegraphics[width=\twidth]{eps/shiftwin}
\caption{Input signal $x$\ (top), third frame
$x_3$\ in its natural time location (middle), and the third frame
shifted to time 0, ${\tilde x}_3$\ (bottom).}
\end{figure}
\end{psfrags}](img1404.png)
Note that we may sample the DTFT of both  and
and
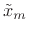 ,
because both are time-limited to
,
because both are time-limited to  nonzero samples. The
minimum information-preserving sampling interval along the unit circle
in both cases is
nonzero samples. The
minimum information-preserving sampling interval along the unit circle
in both cases is
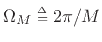 . In practice, we often
oversample to some extent, using
. In practice, we often
oversample to some extent, using 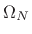 with
with 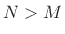 instead. For
instead. For
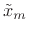 , we get
, we get
where
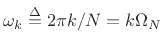 . For
. For 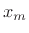 we have
we have
Since
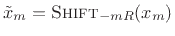 , their transforms are related by the
shift theorem:
, their transforms are related by the
shift theorem:
where 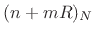 denotes modulo
denotes modulo  indexing (appropriate since the
DTFTs have been sampled at intervals of
indexing (appropriate since the
DTFTs have been sampled at intervals of
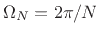 ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() frame back to the time origin:
frame back to the time origin:
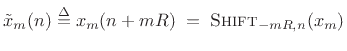
![]() and
and
![]() ,
because both are time-limited to
,
because both are time-limited to ![]() nonzero samples. The
minimum information-preserving sampling interval along the unit circle
in both cases is
nonzero samples. The
minimum information-preserving sampling interval along the unit circle
in both cases is
![]() . In practice, we often
oversample to some extent, using
. In practice, we often
oversample to some extent, using ![]() with
with ![]() instead. For
instead. For
![]() , we get
, we get
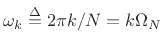 . For
. For 
![]() , their transforms are related by the
shift theorem:
, their transforms are related by the
shift theorem:
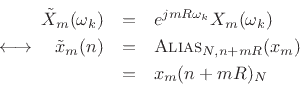
![]() denotes modulo
denotes modulo ![]() indexing (appropriate since the
DTFTs have been sampled at intervals of
indexing (appropriate since the
DTFTs have been sampled at intervals of
![]() ).
).