Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Beginning with a restatement of Eq.(4.9),
we can express each FIR coefficient
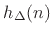 as a vector
expression:
as a vector
expression:
Making a row-vector out of the FIR coefficients gives
or
We may now choose a set of parameter values
![$ {\underline{\Delta}}^T=[\Delta_0,\Delta_1,\ldots,\Delta_L]$](img1096.png) over which an optimum approximation is desired, yielding
the matrix equation
over which an optimum approximation is desired, yielding
the matrix equation
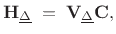 |
(5.11) |
where
Equation (4.11) may be solved for the polynomial-coefficient
matrix
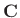 by usual least-squares methods. For example, in the unweighted
case, with
by usual least-squares methods. For example, in the unweighted
case, with
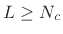 , we have
, we have
Note that this formulation is valid for finding the Farrow
coefficients of any 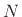 th-order variable FIR filter parametrized by a
single variable
th-order variable FIR filter parametrized by a
single variable 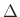 . Lagrange interpolation is a special case
corresponding to a particular choice of
. Lagrange interpolation is a special case
corresponding to a particular choice of
 .
.
In MATLAB, the function fdesign.fracdelay can be used to design
Farrow structures for fractional delay.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
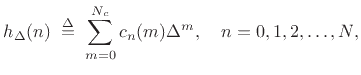
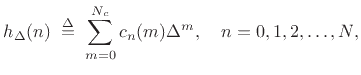
![$\displaystyle h_\Delta(n) \eqsp
\underbrace{%
\left[\begin{array}{ccccc} 1 & \Delta & \Delta^2 & \cdots & \Delta^{N_c}\end{array}\right]}_{\underline{V}_\Delta^T}\,
\left[\begin{array}{c} C_n(0) \\ [2pt] C_n(1) \\ [2pt] \vdots \\ [2pt] C_n({N_c})\end{array}\right]
$](img1093.png)
![$\displaystyle \underbrace{\left[\begin{array}{cccc}h_\Delta(0)\!&\!h_\Delta(1)\!&\!\cdots\!&\!h_\Delta(N)\end{array}\right]}_{\underline{h}_\Delta}
\eqsp
\underline{V}_\Delta^T
\underbrace{
\left[\begin{array}{cccc}
C_0(0) & C_1(0) & \cdots & C_N(0) \\
C_0(1) & C_1(1) & \cdots & C_N(1) \\
\vdots & \vdots & & \vdots \\
C_0({N_c}) & C_1({N_c}) & \cdots & C_N({N_c})
\end{array}\right]}_{\mathbf{C}}
$](img1094.png)
![$\displaystyle \mathbf{H}_{\underline{\Delta}}\isdefs \left[\begin{array}{c} \underline{h}_{\Delta_0}^T \\ [2pt] \vdots \\ [2pt] \underline{h}_{\Delta_L}^T\end{array}\right]
\qquad\mbox{and}\qquad
\mathbf{V}_{\underline{\Delta}}\isdefs \left[\begin{array}{c} \underline{V}_{\Delta_0}^T \\ [2pt] \vdots \\ [2pt] \underline{V}_{\Delta_L}^T\end{array}\right].
$](img1098.png)