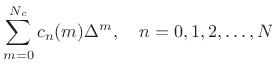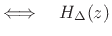Farrow Structure

Taking the z transform of Eq.(4.9) yields

$$h_\Delta(n) \isdef \sum_{m=0}^{N_c}c_n(m)\Delta^m, \quad n=0,1,2,\ldots,N$$

$$\Longleftrightarrow \quad H_\Delta(z) \isdef \sum_{n=0}^N h_\Delta(n)z^{-n}$$

$$= \sum_{n=0}^N \left[\sum_{m=0}^{N_c}c_n(m)\Delta^m\right]z^{-n}$$

$$= \sum_{m=0}^{N_c}\left[\sum_{n=0}^N c_n(m) z^{-n}\right]\Delta^m$$

$$\isdef \sum_{m=0}^{N_c}C_m(z) \Delta^m. \protect$$ (5.10)

Since $H_\Delta(z)$ is an $N$ th-order FIR filter, at least one of the $C_m(z)$ must be $N$ th order, so that we need ${N_c}\ge N$ . A typical choice is ${N_c}=N$ .

When the polynomial Eq.(4.10) is evaluated using Horner's rule,^5.6the efficient Farrow structure [135,506] depicted in Fig.4.19 is obtained. Derivations of Farrow-structure coefficients for Lagrange fractional-delay filtering are introduced in [506, §3.3.7].

Figure 4.19: Farrow structure for implementing parametrized filters as a fixed-filter polynomial in the varying parameter.

As we will see in the next section, Lagrange interpolation can be implemented exactly by the Farrow structure when ${N_c}=N$ . For ${N_c}<N$ , approximations that do not satisfy the exact interpolation property can be computed [].

In summary, the Farrow structure was obtained by writing the variable FIR-filter transfer-function as a polynomial in the control-variable ($\Delta$ above), where the polynomial coefficients are fixed (time-invariant) filters ($C_m(z)$ above). In this form, it is clear that the response of the resulting variable filter is always well defined, being a variable mix of static filters at all times.