Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We will now derive a finite-difference model in terms of string
displacement samples which correspond to the lossy digital waveguide
model of Fig. G.5. This derivation generalizes the lossless case
considered in §G.4.3.
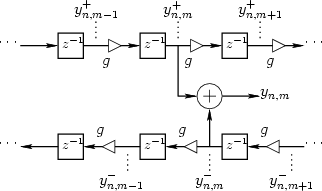
Figure G.7 depicts a digital waveguide section once again in
``physical canonical form,'' as shown earlier in Fig. G.5, and
introduces a doubly indexed notation for greater clarity in the
derivation below
[420,207,116,115].
Figure G.7:
Lossy digital waveguide--frequency-independent loss-factors 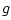 .
.
 |
Referring to Fig. G.7, we have the following time-update
relations:
Adding these equations gives
This is now in the form of the finite-difference time-domain (FDTD)
scheme analyzed in [207]:
with
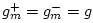 , and
, and 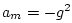 . In
[116], it was shown by von Neumann analysis
(§L.4) that these parameter choices give rise to a stable
finite-difference scheme (§L.2.3), provided
. In
[116], it was shown by von Neumann analysis
(§L.4) that these parameter choices give rise to a stable
finite-difference scheme (§L.2.3), provided 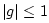 . In the
present context, we expect stability to follow naturally from starting
with a passive digital waveguide model.
. In the
present context, we expect stability to follow naturally from starting
with a passive digital waveguide model.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]