Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Von Neumann Analysis
Von Neumann analysis is used to verify the stability
of a finite difference scheme (FDS). We will only consider FDSs
having one time dimension, but any number of spatial dimensions.
The procedure, in principle, is to perform a spatial Fourier
transform along all spatial dimensions, thereby reducing the FDS to a
time recursion in terms of the spatial Fourier transform of the
system. The system is then stable if this time recursion is at least
marginally stable as a digital filter.
Let's apply von Neumann analysis to the FDS for the ideal vibrating string
Eq. (L.3):
There is only one spatial dimension, so we only need a single 1D
Discrete Time Fourier Transform (DTFT) along 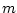 [422].
Using the shift theorem for the DTFT, we obtain
[422].
Using the shift theorem for the DTFT, we obtain
where
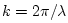 denotes radian spatial frequency (wave number).
(On a more elementary level, the DTFT along
denotes radian spatial frequency (wave number).
(On a more elementary level, the DTFT along 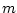 can be carried out by
substituting
can be carried out by
substituting
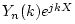 for
for 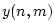 in the FDS.) This is now
a second-order difference equation (digital filter) that needs its
stability checked. This can be accomplished most easily using the
Durbin recursion [426], or we can check that the poles of the
recursion do not lie outside the unit circle in the
in the FDS.) This is now
a second-order difference equation (digital filter) that needs its
stability checked. This can be accomplished most easily using the
Durbin recursion [426], or we can check that the poles of the
recursion do not lie outside the unit circle in the  plane.
plane.
A method equivalent to checking the pole radii, and typically used
when the time recursion is first order, is to compute the
amplification factor as the complex gain 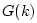 in
the relation
in
the relation
The FDS is then declared stable if
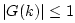 for all spatial
frequencies
for all spatial
frequencies 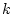 .
.
Since the FDS of the ideal vibrating string is so simple, let's find
the two poles. Taking the z transform of Eq. (L.8) yields
yielding the following characteristic polynomial:
Applying the quadratic formula to find the roots yields
The squared pole moduli are then given by
Thus, for marginal stability, we require
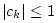 , and the
poles become
Since the range of spatial frequencies is
, and the
poles become
Since the range of spatial frequencies is
![$ k\in[-\pi/X,\pi/X]$](img2900.png) , we
spontaneously have
, we
spontaneously have
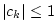 for all
for all 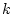 . Therefore, we have shown
by von Neumann analysis that the FDS Eq. (L.3) for the ideal
vibrating string is stable.
. Therefore, we have shown
by von Neumann analysis that the FDS Eq. (L.3) for the ideal
vibrating string is stable.
In summary, von Neumann analysis verifies that no spatial Fourier
components in the system are growing exponentially with respect to
time.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() in
the relation
in
the relation
![$\displaystyle \left\vert z\right\vert^2 = c_k^2 \pm (c_k^2 - 1) =
\left\{\begi...
...eq 1 \\ [5pt]
[1,1], & \left\vert c_k\right\vert\leq 1 \\
\end{array}\right..
$](img2897.png)