The maximally flat fractional-delay FIR filter is obtained by equating
to zero all ![]() leading terms in the Taylor (Maclaurin) expansion of
the frequency-response error at dc:
leading terms in the Taylor (Maclaurin) expansion of
the frequency-response error at dc:
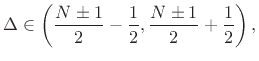

This is a linear system of equations of the form
![\begin{eqnarray*}
\left\vert\left[p_i^{j-1}\right]\right\vert &=& \prod_{j>i}(p_j-p_i)\\
&=&
(p_2-p_1)(p_3-p_1)\cdots(p_N-p_1)\cdots\\
&&(p_3-p_2)(p_4-p_2)\cdots(p_N-p_2)\cdots\\
&&(p_{N-1}-p_{N-2})(p_N-p_{N-2})\cdots\\
&&(p_N-p_{N-1}).
\end{eqnarray*}](img1068.png)
Making this substitution in the solution obtained by Cramer's rule
yields that the impulse response of the order ![]() , maximally flat,
fractional-delay FIR filter may be written in closed form as
, maximally flat,
fractional-delay FIR filter may be written in closed form as

which is the formula for Lagrange-interpolation coefficients (Eq.(4.6)) adapted to this problem (in which abscissae are equally spaced on the integers from 0 to
Further details regarding the theory of Lagrange interpolation can be found in [506, Ch. 3, Pt. 2, pp. 82-84].5.5