![\includegraphics[width=\twidth]{eps/massstringphynum}](img2081.png) |
The previous discussion solved for the motion of an ideal mass striking an ideal string of infinite length. We now investigate the same model from the string's point of view. As before, we will be interested in a digital waveguide (sampled traveling-wave) model of the string, for efficiency's sake (Chapter 6), and we therefore will need to know what the mass ``looks like'' at the end of each string segment. For this we will find that the impedance description (§7.1) is especially convenient.
![\includegraphics[width=\twidth]{eps/massstringphynum}](img2081.png) |
Let's number the string segments to the left and right of the mass by 1 and 2, respectively, as shown in Fig.9.15. Then Eq.(9.8) above may be written
To derive the traveling-wave relations in a digital waveguide model,
we want to use the force-wave variables
![]() and
and
![]() that we defined for vibrating strings in
§6.1.5; i.e., we defined
that we defined for vibrating strings in
§6.1.5; i.e., we defined
![]() , where
, where ![]() is the string tension and
is the string tension and ![]() is the string
slope,
is the string
slope, ![]() .
.
![\includegraphics[width=0.5\twidth]{eps/stringslope}](img2089.png) |
As shown in Fig.9.16, a negative string slope pulls ``up''
to the right. Therefore, at the mass point we have
![]() , where
, where ![]() denotes the position of the
mass along the string. On the other hand, the figure also shows that
a negative string slope pulls ``down'' to the left, so that
denotes the position of the
mass along the string. On the other hand, the figure also shows that
a negative string slope pulls ``down'' to the left, so that
![]() . In summary, relating the forces we
have defined for the mass-string junction to the force-wave variables
in the string, we have
. In summary, relating the forces we
have defined for the mass-string junction to the force-wave variables
in the string, we have
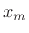
where ![]() denotes the position of the mass along the string.
denotes the position of the mass along the string.
Thus, we can rewrite Eq.(9.11) in terms of string wave variables as
The force relations can be checked individually. For string 1,
states that a positive slope in the string-segment to the left of the mass corresponds to a negative acceleration of the mass by the endpoint of that string segment. Similarly, for string 2,
says that a positive slope on the right accelerates the mass upwards. Similarly, a negative slope pulls ``up'' to the right and ``down'' to the left, as shown in Fig.9.16 above.
Now that we have expressed the string forces in terms of string
force-wave variables, we can derive digital waveguide models by
performing the traveling-wave decompositions
![]() and
and
![]() and using the Ohm's law relations
and using the Ohm's law relations
![]() and
and
![]() for
for ![]() (introduced above near
Eq.(6.6)).
(introduced above near
Eq.(6.6)).