This section discusses use of the Energy Decay Relief (EDR) (§3.2.2) to measure the decay times of the partial overtones in a recorded vibrating string.
First we derive what to expect in the case of a simplified string
model along the lines discussed in §6.7 above. Assume we
have the synthesis model of Fig.6.12, where now the loss
factor ![]() is replaced by the digital filter
is replaced by the digital filter ![]() that we wish
to design. Let
that we wish
to design. Let
![]() denote the contents of the delay line as a
vector at time
denote the contents of the delay line as a
vector at time ![]() , with
, with
![]() denoting the initial contents of the
delay line.
denoting the initial contents of the
delay line.
For simplicity, we define the EDR based on a length ![]() DFT of the delay-line
vector
DFT of the delay-line
vector
![]() , and use a rectangular window with a ``hop size'' of
, and use a rectangular window with a ``hop size'' of ![]() samples,
i.e.,
samples,
i.e.,
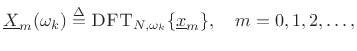
where
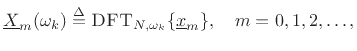 .
That is
.
That is
for each DFT bin number
Applying the definition of the EDR (§3.2.2) to this short-time spectrum gives
![\begin{eqnarray*}
E_m(\omega_k)
&\isdef & \sum_{\nu=m}^\infty \left\vert\underline{X}_\nu(\omega_k)\right\vert^2
\eqsp \sum_{\nu=m}^\infty \left\vert H_l^\nu(\omega_k) \underline{X}_0(\omega_k)\right\vert^2\\ [5pt]
&=& \left\vert\underline{X}_0(\omega_k)\right\vert^2 \sum_{\nu=m}^\infty \left\vert H_l(\omega_k)\right\vert^{2\nu}
\eqsp \left\vert\underline{X}_0(\omega_k)\right\vert^2 \frac{\left\vert H_l(\omega_k)\right\vert^{2m}}{1-\left\vert H_l(\omega_k)\right\vert^2}\\ [5pt]
&=& \frac{\left\vert\underline{X}_0(\omega_k)\right\vert^2}{1-\left\vert H_l(\omega_k)\right\vert^2} \left\vert H_l(\omega_k)\right\vert^{2m}.
\end{eqnarray*}](img1483.png)
We therefore have the following recursion for successive EDR time-slices:7.13
Since we normally try to fit straight-line decays to the EDR on a log scale (typically a decibel scale), we will see the relation
where the common argument
This analysis can be generalized to a time-varying model in which the
loop filter ![]() is allowed to change once per ``period''
is allowed to change once per ``period''
![]() .7.14
.7.14
An online laboratory exercise covering the practical details of measuring overtone decay-times and designing a corresponding loop filter is given in [282].