If ![]() denotes the input to a time-varying delay, the output can be
written as
denotes the input to a time-varying delay, the output can be
written as
where
Let's analyze the frequency shift caused by a time-varying delay by
setting ![]() to a complex sinusoid at frequency
to a complex sinusoid at frequency ![]() :
:
The output is now
The instantaneous phase of this signal is
which can be differentiated to give the instantaneous frequency
 denotes the time derivative
of the delay
denotes the time derivative
of the delay
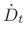
Comparing Eq.(5.6) to Eq.(5.2), we find that the time-varying delay most naturally simulates Doppler shift caused by a moving listener, with
Simulating source motion is also possible, but the relation between delay change and desired frequency shift is more complex, viz., from Eq.(5.2) and Eq.(5.6),

where the approximation is valid for
The time-varying delay line was described in §5.1. As discussed there, to implement a continuously varying delay, we add a ``delay growth parameter'' g to the delayline function in Fig.5.1, and change the line
rptr += 1; // pointer updateto
rptr += 1 - g; // pointer updateWhen g is 0, we have a fixed delay line, corresponding to
to simulate a listener traveling toward the source at speed
Note that when the read- and write-pointers are driven directly from a model of physical propagation-path geometry, they are always separated by predictable minimum and maximum delay intervals. This implies it is unnecessary to worry about the read-pointer passing the write-pointers or vice versa. In generic frequency shifters [277], or in a Doppler simulator not driven by a changing geometry, a pointer cross-fade scheme may be necessary when the read- and write-pointers get too close to each other.