Square Law Series Expansion

When viewed as a Taylor series expansion such as Eq.(6.18), the simplest nonlinearity is clearly the square law nonlinearity:

$$f(x) = x + \alpha x^2$$

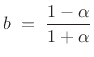where $\alpha$ is a parameter of the mapping.^7.18

Consider a simple signal processing system consisting only of the square-law nonlinearity:

$$y(n) = x(n) + \alpha x^2(n)$$

The Fourier transform of the output signal is easily found using the dual of the convolution theorem:^7.19

$$Y(\omega) = X(\omega) + \alpha (X\ast X)(\omega)$$

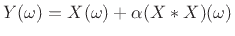where ``$\ast$ '' denotes convolution. In general, the bandwidth of $X\ast X$ is double that of $X$ .