Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Any ``smooth'' function 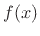 can be expanded as a Taylor series expansion:
can be expanded as a Taylor series expansion:
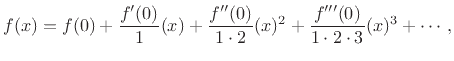 |
(7.18) |
where ``smooth'' means that derivatives of all orders must exist over
the range of validity. Derivatives of all orders are obviously needed
at 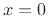 by the above expansion, and for the expansion to be valid
everywhere, the function
by the above expansion, and for the expansion to be valid
everywhere, the function 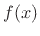 must be smooth for all
must be smooth for all  .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() can be expanded as a Taylor series expansion:
can be expanded as a Taylor series expansion: