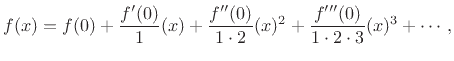
For example, the arctangent function used above can be expanded as
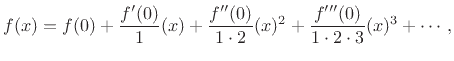
Note that all even-order terms are zero. This is always the case for odd functions, i.e., functions satisfying
The clipping nonlinearity in Eq.(6.17) is not so amenable to a
series expansion. In fact, it is its own series expansion! Since it
is not differentiable at ![]() , it must be represented as three
separate series over the intervals
, it must be represented as three
separate series over the intervals
![]() ,
, ![]() , and
, and
![]() , and the result obtained over these intervals is precisely
the definition of
, and the result obtained over these intervals is precisely
the definition of ![]() in Eq.(6.17).
in Eq.(6.17).