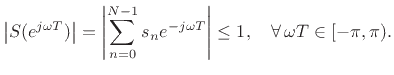Reactive Terminations

In typical string models for virtual musical instruments, the ``nut end'' of the string is rigidly clamped while the ``bridge end'' is terminated in a passive reflectance $S(z)$ . The condition for passivity of the reflectance is simply that its gain be bounded by 1 at all frequencies [450]:

$$\left\vert S(e^{j\omega T})\right\vert\leq 1, \quad \forall\, \omega T\in[-\pi,\pi). \protect$$ (E.42)

A very simple case, used, for example, in the Karplus-Strong plucked-string algorithm, is the two-point-average filter:

$$S(z) = -\frac{1+z^{-1}}{2}$$

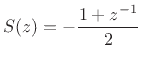
To impose this lowpass-filtered reflectance on the right in the chosen subgrid, we may form

   $$\mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$$$_W=$$   $$\mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$$$_W- \frac{1}{2}{\bm \Delta}_{8,5} - \frac{1}{2}{\bm \Delta}_{8,7}$$

which results in the FDTD transition matrix

$$\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}_K&\isdef & \left[\! \begin{array}{ccccccccccc} 0 & -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & -1 & 1 & -1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 1 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1/2 & -1/2 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1/2 & 1/2 & -1 & -1 \end{array}\!\right]. \end{eqnarray*}$$

This gives the desired filter in a half-rate, staggered grid case. In the full-rate case, the termination filter is really

$$S(z) = -\frac{1+z^{-2}}{2}$$

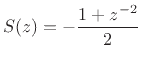
which is still passive, since it obeys Eq.(E.42), but it does not have the desired amplitude response: Instead, it has a notch (gain of 0) at one-fourth the sampling rate, and the gain comes back up to 1 at half the sampling rate. In a full-rate scheme, the two-point-average filter must straddle both subgrids.

Another often-used string termination filter in digital waveguide models is specified by [450]

$$\begin{eqnarray*} s(n) &=& -g\left[\frac{h}{4}, \frac{1}{2}, \frac{h}{4}\right]\\ \longleftrightarrow\quad S(e^{j\omega T})&=& -e^{-j\omega T}g\frac{1 + h \cos(\omega T)}{2}, \end{eqnarray*}$$

where $g\in(0,1)$ is an overall gain factor that affects the decay rate of all frequencies equally, while $h\in(0,1)$ controls the relative decay rate of low-frequencies and high frequencies. An advantage of this termination filter is that the delay is always one sample, for all frequencies and for all parameter settings; as a result, the tuning of the string is invariant with respect to termination filtering. In this case, the perturbation is

   $$\mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}$$$$_W=$$   $$\mbox{$\stackrel{{\scriptscriptstyle \vdash}}{\mathbf{A}}$}$$$$_W- \frac{gh}{4}\delta(M-5,M) - \frac{g}{2}\delta(M-3,M) - \frac{gh}{4}\delta(M-1,M)$$

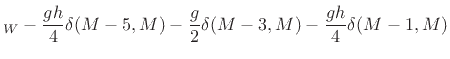
and, using Eq.(E.41), the order $M=8$ FDTD state transition matrix is given by

$$\begin{eqnarray*} \mbox{$\stackrel{{\scriptscriptstyle \vdash\!\!\dashv}}{\mathbf{A}}$}_K&\isdef & \left[\! \begin{array}{ccccccccccc} 0 & -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & -1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & -1 & 1 & -1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1 & 1 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & -1 & 1 & 0 \\ 0 & 0 & g_1 & -g_1 & 1+g_2 & -1-g_2 & 1+g_3 & -1-g_3 \\ 0 & 0 & g_1 & -g_1 & \quad g_2 & \quad -g_2 & \quad g_3 & \quad -g_3 \end{array}\!\right] \end{eqnarray*}$$

where

$$\begin{eqnarray*} g_1 &\isdef & -\frac{gh}{4}\\ g_2 &\isdef & -\frac{g}{2}+g_1\\ g_3 &\isdef & -\frac{gh}{4}+g_2.\\ \end{eqnarray*}$$

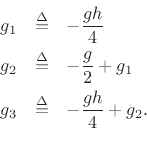
The filtered termination examples of this section generalize immediately to arbitrary finite-impulse response (FIR) termination filters $S(z)$ . Denote the impulse response of the termination filter by

$$s(n)=[s_0,s_1,s_2,\ldots,s_N],$$

where the length $N$ of the filter does not exceed $M/2$ . Due to the DW-FDTD equivalence, the general stability condition is stated very simply as

$$\left\vert S(e^{j\omega T})\right\vert = \left\vert\sum_{n=0}^{N-1} s_n e^{-j\omega T}\right\vert \leq 1, \quad \forall\, \omega T\in[-\pi,\pi).$$