Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
When the delay-line lengths need to be varied in real time, or
interactively in a GUI, it is convenient to choose each delay-line
length 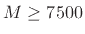 as an integer power of a distinct prime number
as an integer power of a distinct prime number  [458]:
[458]:
where we call 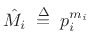 the ``multiplicity'' of the prime
the ``multiplicity'' of the prime  . With
this choice, the delay-line lengths are always coprime (no factors in
common other than
. With
this choice, the delay-line lengths are always coprime (no factors in
common other than 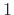 ), and yet we can lengthen or shorten each delay
line individually (by factors of
), and yet we can lengthen or shorten each delay
line individually (by factors of  ) without affecting the mutually
prime property.
) without affecting the mutually
prime property.
Suppose we are initially given desired delay-line lengths 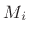 arranged in ascending order so that
arranged in ascending order so that
Then good prime-power approximations 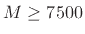 can be expected using
the prime numbers in their natural order:
can be expected using
the prime numbers in their natural order:
Since
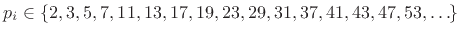 (for any
logarithmic base), an optimal (in some sense) choice of prime
multiplicity
(for any
logarithmic base), an optimal (in some sense) choice of prime
multiplicity 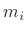 is
is
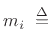
round
![$\displaystyle \left[\frac{\log(M_i)}{\log(p_i)}\right]
\isdefs \left\lfloor 0.5 + \frac{\log(M_i)}{\log(p_i)}\right\rfloor.
$](img807.png)
where 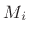 is the desired length in samples. That is,
is the desired length in samples. That is, 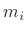 can be
simply obtained by rounding
can be
simply obtained by rounding
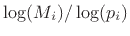 to the
nearest integer (max 1). The prime-power delay-line length
approximation is then of course
to the
nearest integer (max 1). The prime-power delay-line length
approximation is then of course
and the multiplicative approximation error is bounded by
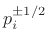 (when
(when
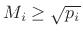 ).
).
This prime-power length scheme is used to keep 16 delay lines both
variable and mutually prime in Faust's reverb_designer.dsp
programming example (via the function prime_power_delays in
effect.lib).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() as an integer power of a distinct prime number
as an integer power of a distinct prime number ![]() [458]:
[458]:
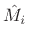
![]() arranged in ascending order so that
arranged in ascending order so that
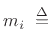 round
round![$\displaystyle \left[\frac{\log(M_i)}{\log(p_i)}\right]
\isdefs \left\lfloor 0.5 + \frac{\log(M_i)}{\log(p_i)}\right\rfloor.
$](img807.png)