Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A lossless prototype reverberator, as in Fig.3.10 when 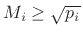 ,
has all of its poles on the unit circle in the
,
has all of its poles on the unit circle in the 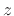 plane, and its
reverberation time is infinity. To set the reverberation time to a
desired value, we need to move the poles slightly inside the unit
circle. Furthermore, due to air absorption
(§2.3,§B.7.15), we want the high-frequency
poles to be more damped than the low-frequency poles
[317]. As discussed in §2.3, this type
of transformation can be obtained using the substitution
plane, and its
reverberation time is infinity. To set the reverberation time to a
desired value, we need to move the poles slightly inside the unit
circle. Furthermore, due to air absorption
(§2.3,§B.7.15), we want the high-frequency
poles to be more damped than the low-frequency poles
[317]. As discussed in §2.3, this type
of transformation can be obtained using the substitution
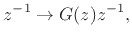 |
(4.5) |
where 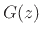 denotes the filtering per sample in the
propagation medium (a lowpass filter with gain not exceeding 1 at all
frequencies).4.15Thus, to set the FDN reverberation time to
denotes the filtering per sample in the
propagation medium (a lowpass filter with gain not exceeding 1 at all
frequencies).4.15Thus, to set the FDN reverberation time to
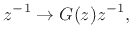 at frequency
at frequency 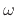 ,
we want propagation through
,
we want propagation through 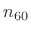 samples to result in attenuation
by
samples to result in attenuation
by 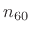 dB, i.e.,
dB, i.e.,
![$\displaystyle \left[G(e^{j\omega T})\right]^{n_{60}(\omega)} \eqsp 0.001. \protect$](img817.png) |
(4.6) |
Solving for 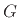 , the propagation attenuation per-sample, gives
, the propagation attenuation per-sample, gives
The last form comes from
 ln
ln , where
, where
 denotes the time constant of decay (time to decay by
denotes the time constant of decay (time to decay by 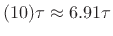 )
[454], i.e.,
)
[454], i.e.,
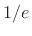 ln ln |
(4.8) |
Series expanding
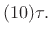 and assuming
and assuming
 samples (
samples (
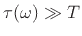 seconds) provides the practically useful approximation
seconds) provides the practically useful approximation
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ,
has all of its poles on the unit circle in the
,
has all of its poles on the unit circle in the ![]() plane, and its
reverberation time is infinity. To set the reverberation time to a
desired value, we need to move the poles slightly inside the unit
circle. Furthermore, due to air absorption
(§2.3,§B.7.15), we want the high-frequency
poles to be more damped than the low-frequency poles
[317]. As discussed in §2.3, this type
of transformation can be obtained using the substitution
plane, and its
reverberation time is infinity. To set the reverberation time to a
desired value, we need to move the poles slightly inside the unit
circle. Furthermore, due to air absorption
(§2.3,§B.7.15), we want the high-frequency
poles to be more damped than the low-frequency poles
[317]. As discussed in §2.3, this type
of transformation can be obtained using the substitution
![\begin{eqnarray*}
e^{-T/\tau(\omega)}
&\!=\!& 1 - \frac{T}{\tau(\omega)} + \frac{1}{2!}\left[\frac{T}{\tau(\omega)}\right]^2 - \cdots
\approxs 1 - \frac{3\mbox{ln}(10)}{n_{60}}
\approxs 1 - \frac{6.91}{n_{60}}.
\end{eqnarray*}](img830.png)