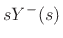 |
The previous section treated an ideal point-mass striking an ideal string. This can be considered a simplified piano-hammer model. The model can be improved by adding a damped spring to the point-mass, as shown in Fig.9.22 (cf. Fig.9.12).
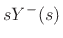 |
The impedance of this plucking system, as seen by the string, is the
parallel combination of the mass impedance ![]() and the damped spring
impedance
and the damped spring
impedance ![]() . (The damper
. (The damper ![]() and spring
and spring ![]() are formally
in series--see §7.2, for a refresher on series versus
parallel connection.) Denoting
the driving-point impedance of the hammer at the string contact-point
by
are formally
in series--see §7.2, for a refresher on series versus
parallel connection.) Denoting
the driving-point impedance of the hammer at the string contact-point
by ![]() , we have
, we have
The impedance formulation of Eq.(9.19) assumes all elements are linear and time-invariant (LTI), but in practice one can normally modulate element values as a function of time and/or state-variables and obtain realistic results for low-order elements. For this we must maintain filter-coefficient formulas that are explicit functions of physical state and/or time. For best results, state variables should be chosen so that any nonlinearities remain memoryless in the digitization [364,351,560,558].