Including Hysteresis

Since the compressed hammer-felt (wool) on real piano hammers shows significant hysteresis memory, an improved piano-hammer felt model is

$$f_h(t) \eqsp Q_0\left[x_k^p + \alpha \frac{d(x_k^p)}{dt}\right], \protect$$ (10.21)

where $\alpha = 248 + 1.83\,n - 5.5 \cdot 10^{-2}n^2$ ($\mu$ s), and again $n$ denotes piano key number [490].

Equation (9.21) is said to be a good approximation under normal playing conditions. A more complete hysteresis model is [490]

$$f_h(t) \eqsp f_0\left[x_k^p(t) - \frac{\epsilon}{\tau_0} \int_0^t x_k^p(\xi) \exp\left(\frac{\xi-t}{\tau_0}\right)d\xi\right]$$

where

$$\begin{eqnarray*} f_0 &=& \mbox{ instantaneous hammer stiffness}\\ \epsilon &=& \mbox{ hysteresis parameter}\\ \tau_0 &=& \mbox{ hysteresis time constant}. \end{eqnarray*}$$

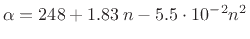
Relating to Eq.(9.21) above, we have $Q_0=f_0\cdot(1-\epsilon)$ (N/mm$\null^p$ ).